系列文章
-> A算法初探究及优化 - 自动解贪吃蛇
A算法深入探究 - 使用Qt和C++实现带权重版本的A*
A算法扩展 - 三维A

说起来，贪吃蛇游戏好像贯穿了我的编程学习之路。

  • 大一时候，用单片机点亮了一个8x8的LED阵列，配合上下左右四个按键，在C51平台写了自己所理解的贪吃蛇版本。以至于大二当上了光协技术部部长时也把“调通我提供的贪吃蛇框架代码、自己再实现部分特殊功能”作为学校电子竞赛软件类的题目用来“迫害”学弟学妹们。
  • 之后参加电赛，暑假准备期间，为了让到正式比赛时我们的作品能有很好的界面以及交互，开始调一块4.7寸的电容屏，在STM32平台上编写自己的图形框架。框架编写得很顺利，所以开始写程序玩，又想到了贪吃蛇！可是现在只有触屏，要是照着手机的策略，加上虚拟按键搓屏幕，总觉得不够优雅。要不让贪吃蛇自己动起来吧！想了一些方案，当时也还不知道有A*算法，用DFS写出了自己的第一个自动贪吃蛇版本。角色互换，玩家通过触屏控制食物的生成，计算机来控制蛇寻找食物并吃掉。
  • 学习python的过程中，接触到了pygame，又把之前在MCU的自动贪吃蛇用python实现了一遍。
  • 工作的时候，为了提升自己的工作效率，下班后开发了几个开发工具（后来这三个工具成了组里面以至于部门里面绝对的流行哈哈哈，以后可以聊聊这个话题）。开发得差不多了，就想着往里面添加彩蛋，毕竟这些程序是我自己的，不是公司里面的。这时候在用得最频繁的上位机上面实现了C#版本的自动贪吃蛇，引入了A*算法，并且图形也不再是一个个方块了，而是使用折线来绘制蛇身，可以连续移动。
  • 考研期间有花一部分时间用来学unity，又想到了这个项目，于是想做一个最终的版本，这个版本会有卓越的性能优化，也有简洁漂亮的外观。也就是今天要讲述的版本。

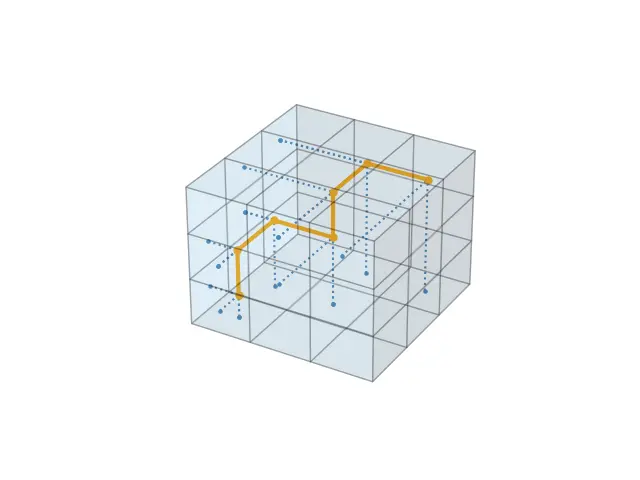
网格

在使用A*进行寻路之前，得将地图进行网格化，网格的大小决定了寻路的精度。另一方面正好经典的贪吃蛇游戏是在网格上进行游玩的。

若遇到连续地图的游戏，可以先对地图进行预处理：即以一定的间隔对地图进行采样，如果以采样点为中心的一定范围内出现了不可达区域，则将该采样点对应的网格设置为不可行走。
当然，对于贪吃蛇游戏来说，地图只有可达与不可达两种状态。若是对于一般游戏，可以细分该“可达性”参数，称为“行走代价”。这样就可以达到寻路时优先沿着道路行走的效果了。

网格划分

在场景中添加空物体，起名为GridController，为其添加GridController.cs脚本。

其中与建立网格相关代码如下：
GridController.cs

1
2
3
4
5
6
private void Awake()
{
    CreateGrid();

    RefreshGrid();
}

CreateGrid方法用来创建网格节点。
其中mapSize是可以在编辑器里面修改的量，也可以后续运行过程中由UI修改，代表网格大小；AStar.Node类中有A*算法需要的数据，GridCoordToWorldPosition是坐标转换函数，后续坐标转换章节会讲到；AdjustWalls将网格的边界扩展至mapSize大小。
GridController.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public Coord mapSize = new(10, 10);

AStar.Node[,] grid;

void CreateGrid()
{
    grid = new AStar.Node[mapSize.x, mapSize.y];

    for (int x = 0; x < mapSize.x; x++)
    {
        for (int y = 0; y < mapSize.y; y++)
        {
            grid[x, y] = new AStar.Node(true, GridCoordToWorldPosition(x, y), x, y);
        }
    }

    AdjustWalls(mapSize.x, mapSize.y);
}

RefreshGrid方法会清除上一次使用A*算法时对grid带来的改变。
GridController.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void RefreshGrid()
{
    for (int x = 0; x < mapSize.x; x++)
    {
        for (int y = 0; y < mapSize.y; y++)
        {
            AStar.Node currentNode = grid[x, y];
            currentNode.walkable = true;
            currentNode.gCost = 0;
            currentNode.hCost = 0;
            currentNode.parent = null;
        }
    }
}

AdjustWalls方法中，walls和background都是在编辑器中设置，当每次网格变化时，该方法会调整边界以匹配网格。后续发现使用专门的相机来渲染背景会比现在这个方法优雅很多，等“贪吃蛇”章节再讲。
GridController.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public Transform[] walls;
public Transform background;

public void AdjustWalls(int sizeX, int sizeY)
{
    float wallPositionX = sizeX / 2f + .5f;
    walls[0].position = Vector3.left * wallPositionX;
    walls[1].position = Vector3.right * wallPositionX;
    Vector3 tallWallScale = Vector3.up * (sizeY - 1) + Vector3.one;
    walls[0].localScale = tallWallScale;
    walls[1].localScale = tallWallScale;

    float wallPositionY = sizeY / 2f + .5f;
    walls[2].position = Vector3.up * wallPositionY;
    walls[3].position = Vector3.down * wallPositionY;
    Vector3 fatWallScale = Vector3.right * (sizeX + 1) + Vector3.one;
    walls[2].localScale = fatWallScale;
    walls[3].localScale = fatWallScale;

    background.localScale = tallWallScale - Vector3.up + fatWallScale - 3 * Vector3.right;
}

坐标转换

坐标转换分为两种，一种是网格坐标和世界坐标的互相转换，另一种是网格坐标和一维坐标的转换。
网格坐标转换为一维坐标主要是给并查集使用的。
GridController.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public Coord WorldPositionToGridCoord(Vector3 worldPos)
{
    int coordX = Mathf.RoundToInt(worldPos.x / gridSize + (mapSize.x - 1) / 2f);
    int coordY = Mathf.RoundToInt(worldPos.y / gridSize + (mapSize.y - 1) / 2f);
    return new(coordX, coordY);
}

public Vector3 GridCoordToWorldPosition(Coord coord)
{
    return GridCoordToWorldPosition(coord.x, coord.y);
}

public Vector3 GridCoordToWorldPosition(int x, int y)
{
    float worldX = x * gridSize - (mapSize.x - 1) * gridSize / 2f;
    float worldY = y * gridSize - (mapSize.y - 1) * gridSize / 2f;
    return new Vector3(worldX, worldY, 0);
}

public int CoordToIndex(int x, int y)
{
    return y * mapSize.x + x;
}

public int CoordToIndex(Coord coord)
{
    return CoordToIndex(coord.x, coord.y);
}

public Coord IndexToCoord(int idx)
{
    return new Coord(idx % mapSize.x, idx / mapSize.x);
}

其中Coord是一个整数坐标的类：
GridController.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
[System.Serializable]
public struct Coord
{
    public int x;
    public int y;

    public Coord(int _x, int _y)
    {
        x = _x;
        y = _y;
    }

    public static bool operator ==(Coord a, Coord b)
    {
        return a.x == b.x && a.y == b.y;
    }

    public static bool operator !=(Coord a, Coord b)
    {
        return !(a == b);
    }

    public override bool Equals(object obj)
    {
        return base.Equals(obj);
    }

    public override int GetHashCode()
    {
        return base.GetHashCode();
    }

    public static Coord operator +(Coord a, Vector2 b)
    {
        return new(a.x + (int)b.x, a.y + (int)b.y);
    }

    public static Coord operator +(Coord a, Coord b)
    {
        return new(a.x + b.x, a.y + b.y);
    }
}

并查集

A*算法虽然高效，但是每次都需要刷新所有网格节点以清除A*算法的临时数据，而且如果两个节点之间不存在路径，A*算法需要将起点所在连通域里面所有的节点都遍历完。
对于这个项目来说，并不是所有寻路任务都需要寻找到确切的一条路径的，而是判断两个点是连通着的就好了。并查集可以很好的完成这个任务，而且因为没有临时数据，维护一次并查集可以反复使用。
GridController中提供了检查两个点是否连通的策略。刷新并查集时，每遍历到一个节点，如果该节点可以行走，就看与之直接连通的左边节点和右边节点是否可以行走，如果可以则合并两个集合。判断是否连通时，只要两个节点追踪到最顶层时发现是在同一个集合中，就可以判断两个节点之间一定存在某条路径。
GridController.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public UFSet set { get; private set; }

void CreateGrid()
{
    set = new(gridCount);
}

public void RefreshSet()
{
    set.Init();

    for (int x = 0; x < mapSize.x; x++)
    {
        for (int y = 0; y < mapSize.y; y++)
        {
            if (grid[x, y].walkable)
            {
                Coord currentCoord = new Coord(x, y) + Vector2.left;
                if (IsCoordInsideGrid(currentCoord) && grid[currentCoord.x, currentCoord.y].walkable)
                {
                    set.Union(CoordToIndex(x, y), CoordToIndex(currentCoord));
                }
                currentCoord = new Coord(x, y) + Vector2.up;
                if (IsCoordInsideGrid(currentCoord) && grid[currentCoord.x, currentCoord.y].walkable)
                {
                    set.Union(CoordToIndex(x, y), CoordToIndex(currentCoord));
                }
            }
        }
    }
}

public bool IsConnected(AStar.Node startNode, AStar.Node targetNode)
{
    return set.Find(CoordToIndex(startNode.gridCoord)) == set.Find(CoordToIndex(targetNode.gridCoord));
}

bool IsCoordInsideGrid(Coord coord)
{
    return IsCoordInsideGrid(coord.x, coord.y);
}

bool IsCoordInsideGrid(int x, int y)
{
    if (x < 0 || y < 0 || x >= mapSize.x || y >= mapSize.y) return false;
    return true;
}

并查集的类需要自己编写，这里用了一些平衡的方式，使得并查集搜索时不至于太大的深度。
UFSet.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public class UFSet
{
    public int[] parent { get; private set; }
    private int[] rank;

    public UFSet(int n)
    {
        parent = new int[n];
        rank = new int[n];
        Init();
    }

    public void Init()
    {
        for (int i = 0; i < parent.Length; i++)
        {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    public bool Union(int a, int b)
    {
        int rootA = Find(a);
        int rootB = Find(b);

        if (rootA == rootB) return false;

        if (rank[rootA] < rank[rootB])
        {
            parent[rootA] = rootB;
        }
        else
        {
            parent[rootB] = rootA;
            if (rank[rootA] == rank[rootB]) rank[rootA]++;
        }
        return true;
    }

    public int Find(int p)
    {
        if (parent[p] != p)
            parent[p] = Find(parent[p]);
        return parent[p];
    }

    public bool IsConnected(int a, int b)
    {
        return parent[a] == parent[b];
    }
}

提供的服务

GridController中会处理玩家输入，即让玩家在网格中任意位置点击鼠标时可以生成食物。为了让程序自动运行时也能有进展，GridController中也实现了自动生成食物的功能。使用洗牌算法来随机排列可行走的网格，当没有食物时从随机排列的列表中选择第一个作为食物生成的节点。
GridController.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public Food foodPrefab;

[HideInInspector]
public List<Food> foods;
Queue<AStar.Node> shuffledWalkableNodes;

private void Update()
{
    Vector3 mousePos = Camera.main.ScreenToWorldPoint(Input.mousePosition);
    cursor.transform.position = new Vector3(mousePos.x, mousePos.y, 0);

    if (Input.GetMouseButtonDown(0))
    {
        Coord foodCoord = WorldPositionToGridCoord(cursor.position);
        if (IsCoordInsideGrid(foodCoord))
        {
            AStar.Node foodNode = GetNodeFromCoord(foodCoord);
            if (foodNode.walkable)
            {
                CreateFood(cursor.position);
            }
        }
    }
}

void CreateFood(Vector3 position)
{
    Food newFood = Instantiate(foodPrefab, position, Quaternion.identity);
    newFood.transform.SetParent(transform, false);
    newFood.OnFoodAte += OnFoodAte;
    newFood.SetNode(GetNodeFromWorldPosition(position));
    foods.Add(newFood);
}

void OnFoodAte(Food food)
{
    foods.Remove(food);
    Destroy(food.gameObject);
}

public void RefreshWalkableList()
{
    List<AStar.Node> walkableNodes = new();
    for (int x = 0; x < mapSize.x; x++)
    {
        for (int y = 0; y < mapSize.y; y++)
        {
            if (grid[x, y].walkable) walkableNodes.Add(grid[x, y]);
        }
    }
    shuffledWalkableNodes = new Queue<AStar.Node>(Utility.ShuffleArray(walkableNodes.ToArray()));

    if (autoGenerateFood && foods.Count == 0)
    {
        CreateFood(GetRandomWalkableNode().worldPosition);
    }
}

其他类有时需要根据各种方式获得一个（些）网格节点，GridController中应该创建对应的方法。
GridController.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public AStar.Node GetNode(Coord coord)
{
    return grid[coord.x, coord.y];
}

public AStar.Node GetRandomWalkableNode()
{
    AStar.Node randomNode = shuffledWalkableNodes.Dequeue();
    shuffledWalkableNodes.Enqueue(randomNode);
    return randomNode;
}

public AStar.Node[] GetNeighbours(AStar.Node node)
{
    List<AStar.Node> neighbours = new List<AStar.Node>();

    for (int x = -1; x <= 1; x++)
    {
        for (int y = -1; y <= 1; y++)
        {
            if ((x == 0 || y == 0) && x != y)
            {
                Coord coordDelta = new(x, y);
                Coord checkCoord = node.gridCoord + coordDelta;
                if (IsCoordInsideGrid(checkCoord))
                {
                    neighbours.Add(grid[checkCoord.x, checkCoord.y]);
                }
            }
        }
    }

    return neighbours.ToArray();
}

public AStar.Node GetNodeFromCoord(Coord coord)
{
    if (!IsCoordInsideGrid(coord)) return null;
    return grid[coord.x, coord.y];
}

public AStar.Node GetNodeFromCoord(int x, int y)
{
    if (!IsCoordInsideGrid(x, y)) return null;
    return grid[x, y];
}

public AStar.Node GetNodeFromWorldPosition(Vector3 position)
{
    return GetNodeFromCoord(WorldPositionToGridCoord(position));
}

网格大小在UI中动态可调，调整时需要重建网格，也需要调整网格边界的显示。
GridController.cs

1
2
3
4
5
6
7
8
9
10
public void SetMapSize(int x, int y)
{
    if (x < minMapSize.x) x = minMapSize.x;
    if (y < minMapSize.y) y = minMapSize.y;

    mapSize.x = x;
    mapSize.y = y;

    CreateGrid();
}

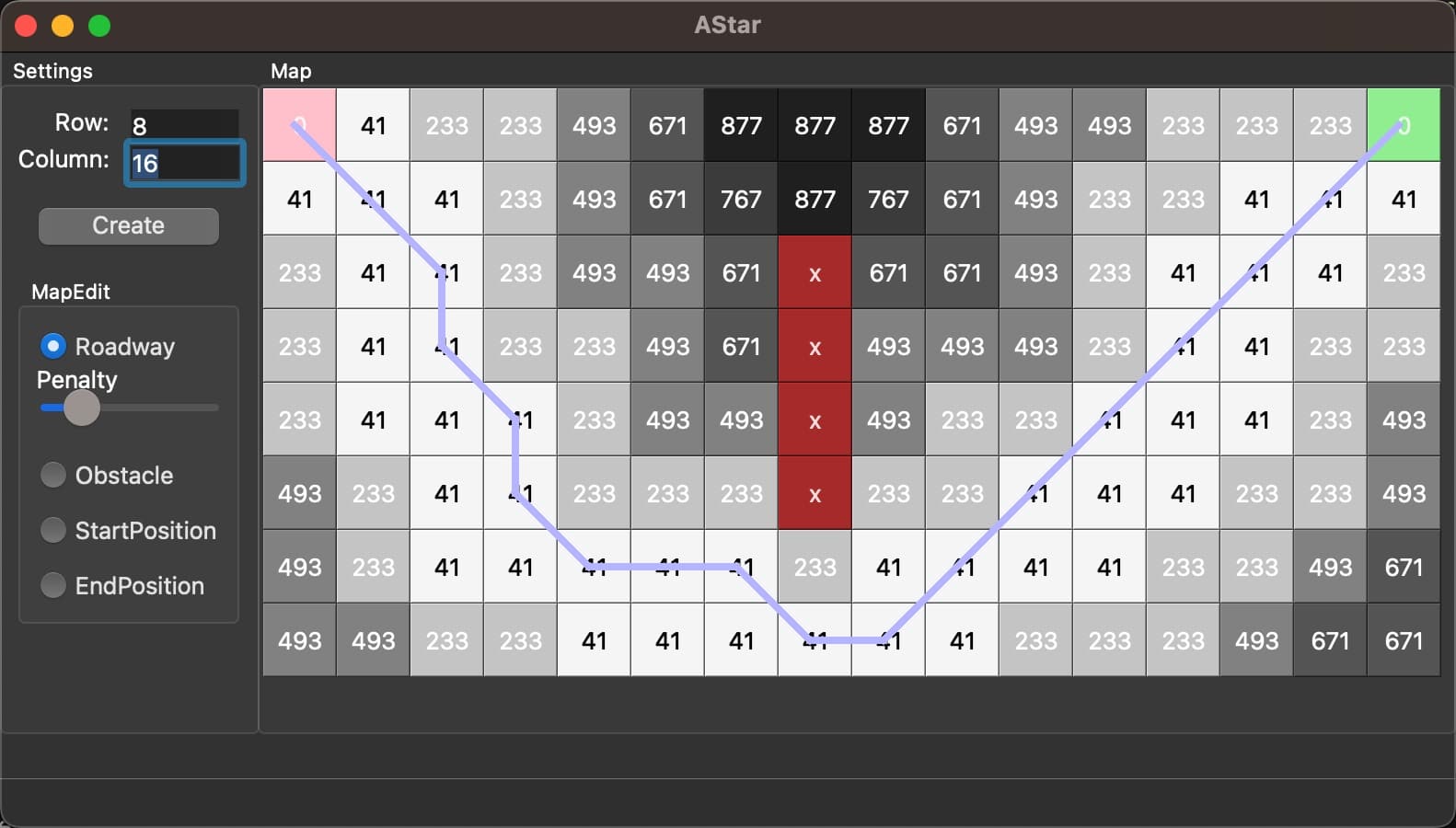
A*

去搜索A*算法的话，很多教程一上来就开始推导运行过程，不先讲为什么这么推导，导致我开始学A*的时候感到特别困惑。
其实了解完了之后，A*算法的思路特别简单：我们的目标是寻找一条从起点到终点，代价最小的路径。既然有了标准，那么我们在遍历节点时，就不应该盲目地遍历，而是应该挑那些“最有可能代价很小”的节点来运算。
如何获得这种节点呢，这就是启发函数要做的事情。代价无非就是起点到终点的路线长度，可是没有找到路的时候，我们该如何计算这个代价呢？
把代价分为两个方面：

  • 已经知道的代价。即从起点到当前节点已经走过的路线长度。
  • 未来可能会有的代价。用“猜”的，假设从当前节点到目标节点没有障碍，代价会是多少。

知道启发函数是怎么回事之后我们就可以开始遍历节点了。从起点开始，计算其四周节点的代价，并把那些节点放到一个“池子”里面去，之后每次都从池子里面捞出来代价最小的节点，继续计算其周围节点的代价。
如果遍历到目标节点，或者池子空了之后，寻路就结束了。那么如何获得路径呢？我们遍历的过程可以看出，节点加入到池子之前，我们知道这些加入到池子中的节点是来自于当前节点的，所以在加入池子之前将那些节点的父节点设为当前节点，等寻路到目标节点之后我们逐个节点遍历其父节点，就可以遍历完最短路径。

至于算法优化，有如下几点细节：

  • 计算当前节点的周围节点的代价值时，如果需计算的节点原先就已经算过代价值，而当前算出来的代价值比原先的小，说明这个节点从当前节点过去路径会更短一些，应当刷新其父节点和代价值。
  • 我们之前说“池子”的时候，有提到每次需要从中找出代价最小的节点用来计算，而小根堆有很高效的寻找最小值元素的特性，所以将“池子”用小根堆来组织。

算法实现

定义算法所需要的节点类，其中IHeapItem是用来后续实现堆时能够让堆接收自定义的AStar.Node类作为堆中的元素。
AStar.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class Node : IHeapItem<Node>
{
    public bool walkable;
    public Vector3 worldPosition;
    public GridController.Coord gridCoord;

    public int gCost;
    public int hCost;
    public int fCost { get { return gCost + hCost; } }

    public Node parent;

    int heapIndex;

    public Node(bool _walkable, Vector3 _worldPos, int _gridX, int _gridY)
    {
        walkable = _walkable;
        worldPosition = _worldPos;
        gridCoord = new(_gridX, _gridY);
    }

    public int HeapIndex
    {
        get { return heapIndex; }
        set { heapIndex = value; }
    }

    public int CompareTo(Node nodeToCompare)
    {
        int compare = fCost.CompareTo(nodeToCompare.fCost);
        if (compare == 0) compare = hCost.CompareTo(nodeToCompare.hCost);
        return -compare;
    }
}

寻路算法的实现如下：
AStar.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
GridController grid;

private void Awake()
{
    grid = GetComponent<GridController>();
}

public Node[] FindPath(Node startNode, Node targetNode)
{
    Heap<Node> openSet = new Heap<Node>(grid.gridCount);
    HashSet<Node> closedSet = new HashSet<Node>();

    openSet.Add(startNode);
    while (openSet.Count > 0)
    {
        Node currentNode = openSet.RemoveFirst();

        closedSet.Add(currentNode);

        if (currentNode == targetNode)
        {
            return RetracePath(startNode, targetNode);
        }

        foreach (Node neighbour in Utility.ShuffleArray(grid.GetNeighbours(currentNode)))
        {
            if (!neighbour.walkable || closedSet.Contains(neighbour)) continue;

            int newMovementCostToNeighbour = currentNode.gCost + GetDistance(currentNode, neighbour);
            if (newMovementCostToNeighbour < neighbour.gCost || !openSet.Contains(neighbour))
            {
                neighbour.gCost = newMovementCostToNeighbour;
                neighbour.hCost = GetDistance(neighbour, targetNode);
                neighbour.parent = currentNode;

                if (!openSet.Contains(neighbour))
                {
                    openSet.Add(neighbour);
                }
            }
        }
    }
    return null;
}

int GetDistance(Node nodeA, Node nodeB)
{
    return Mathf.Abs(nodeA.gridCoord.x - nodeB.gridCoord.x) + Mathf.Abs(nodeA.gridCoord.y - nodeB.gridCoord.y);
}

输出寻得的路径的代码如下：
AStar.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Node[] RetracePath(Node startNode, Node endNode)
{
    List<Node> path = new List<Node>();
    Node currentNode = endNode;

    while (currentNode != startNode)
    {
        path.Add(currentNode);
        currentNode = currentNode.parent;
    }

    path.Reverse();

    return path.ToArray();
}

堆

C#中没有可以使用的现成的堆，需要自己编写。思路是将堆编写为模板类，要求其元素需实现IHeapItem接口。
对于小根堆来说，其满足的条件是任意节点的子树中所有节点都大于该节点。这个要求是在每次插入元素到堆中，或者从堆中删除根节点时对堆的调整来实现的。
插入的元素一开始必定在叶节点中，通过一层层“上浮”让新插入的节点移动到正确的位置。删除根节点时也需要让新的根节点一层层“下沉”到达正确的位置。
Heap.cs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
public class Heap<T> where T : IHeapItem<T>
{
    T[] items;
    int currentItemCount;

    public Heap(int maxHeapSize)
    {
        items = new T[maxHeapSize];
    }

    public void Add(T item)
    {
        item.HeapIndex = currentItemCount;
        items[currentItemCount] = item;
        SortUp(item);
        currentItemCount++;
    }

    public T RemoveFirst()
    {
        T firstItem = items[0];
        currentItemCount--;
        items[0] = items[currentItemCount];
        items[0].HeapIndex = 0;
        SortDown(items[0]);
        return firstItem;
    }

    public void UpdateItem(T item)
    {
        SortUp(item);
        SortDown(item);
    }

    public int Count { get { return currentItemCount; } }

    public bool Contains(T item)
    {
        return Equals(items[item.HeapIndex], item);
    }

    void SortDown(T item)
    {
        while (true)
        {
            int childIndexLeft = item.HeapIndex * 2 + 1;
            int childIndexRight = item.HeapIndex * 2 + 2;

            int swapIndex;
            if (childIndexLeft < currentItemCount)
            {
                swapIndex = childIndexLeft;
                if (childIndexRight < currentItemCount)
                {
                    if (items[childIndexLeft].CompareTo(items[childIndexRight]) < 0)
                    {
                        swapIndex = childIndexRight;
                    }
                }

                if (item.CompareTo(items[swapIndex]) < 0)
                {
                    Swap(item, items[swapIndex]);
                }
                else
                {
                    return;
                }
            }
            else
            {
                return;
            }
        }
    }

    void SortUp(T item)
    {
        int parentIndex = (item.HeapIndex - 1) / 2;

        while (true)
        {
            T parentItem = items[parentIndex];
            if (item.CompareTo(parentItem) > 0)
            {
                Swap(item, parentItem);
            }
            else
            {
                break;
            }

            parentIndex = (item.HeapIndex - 1) / 2;
        }
    }

    void Swap(T itemA, T itemB)
    {
        items[itemA.HeapIndex] = itemB;
        items[itemB.HeapIndex] = itemA;
        int itemAIndex = itemA.HeapIndex;
        itemA.HeapIndex = itemB.HeapIndex;
        itemB.HeapIndex = itemAIndex;
    }
}

public interface IHeapItem<T> : IComparable<T>
{
    int HeapIndex
    {
        get;
        set;
    }
}

贪吃蛇

存储

显示

动画

Wander

生长

决策