GuoFan

系列文章 -> A算法初探究及优化 - 自动解贪吃蛇 A算法深入探究 - 使用Qt和C++实现带权重版本的A* A算法扩展 - 三维A 说起来，贪吃蛇游戏好像贯穿了我的编程学习之路。 大一时候，用单片机点亮了一个8x8的LED阵列，配合上下左右四个按键，在C51平台写了自己所理解的贪吃蛇版本。以至于大二当上了光协技术部部长时也把“调通我提供的贪吃蛇框架代码、自己再实现部分特殊功能”作为学校电子竞赛软件类的题目用来“迫害”学弟学妹们。 之后参加电赛，暑假准备期间，为了让到正式比赛时我们的作品能有很好的界面以及交互，开始调一块4.7寸的电容屏，在STM32平台上编写自己的图形框架。框架编写得很顺利，所以开始写程序玩，又想到了贪吃蛇！可是现在只有触屏，要是照着手机的策略，加上虚拟按键搓屏幕，总觉得不够优雅。要不让贪吃蛇自己动起来吧！想了一些方案，当时也还不知道有A*算法，用DFS写出了自己的第一个自动贪吃蛇版本。角色互换，玩家通过触屏控制食物的生成，计算机来控制蛇寻找食物并吃掉。 学习python的过程中，接触到了pygame，又把之前在MCU的自动贪吃蛇用python实现了 ...

系列文章 -> GAMES101笔记 - Resterization（光栅化） GAMES101笔记 - Shading（着色） GAMES101笔记 - Geometry（几何） 20年的时候，好朋友推荐了这个课程给我，简直是神仙课程！当时每天下班后就再花一个多小时来听一节课，陆陆续续听完了。最近打算重温一下这系列课程，顺便补上笔记。 图形学有一种魔力，每次学图形学相关的知识的时候，总在感叹其美妙。第一次系统地学习图形学是在大三，当时智能车已经进入了平稳的调试期，所以找了一些囤积起来的一直想学的技术书籍开始学习：Golang、图形学、Unity3D等等。 学到图形学的时候，正好智能车这边在调试利用陀螺仪对坡道的识别，所以突发奇想：在屏幕上显示一个3D图形，然后把陀螺仪解算出来的姿态实时绑定到3D图形上面，会比单纯地看上位机展示出来的陀螺仪数据曲线要来的直观很多吧！于是有了这个玩意： 线代知识点回顾 向量 a⃗=(xa,ya,za)Tb⃗=(xb,yb,zb)T\begin{aligned} \vec{a} &= (x_a, y_a, z_a)^T \\ \vec ...

2025 在 AI Coding 领域来说是飞速发展的一年，一路使用过来，感叹与AI成长之迅速。年初的时候还是蹬一步走一步的自行车呢，到年底已经变成可以设置一个导航就自动开往目的地的自动驾驶汽车了。 年初，claude 3.7 发布，借着 copilot 的 edit 模式，一周之内完整移植了一整套 1w 行左右的代码，当时看着编辑器里面每秒冒出好几行代码的速度，同事们纷纷过来录像分享。这一典型案例也被后续分享到了全公司。 cline、roo code 等 vscode 插件的发布，agent 时代正式到来，这一期间我已经逐渐把 ai agent 当作一个实习生使用了，为每个项目仓库建立了 memory-bank，简单的需求写好提示词直接运行。开好多个 vscode 窗口，并行跑好多开发任务。从这个时期开始，我已经基本不使用搜索引擎了，知识类的交互交给 chat，执行类的任务交给 agent。 今年最重磅的事情我还是颁发给 claude code 和 qwen coder，一个是 coding 领域的王者 agent，另一个则物美价廉。任务来了，首先描述一遍需求，让 agent 先试一 ...

本篇是对 ROS 官方 Tutorials “初级教程 8-16”部分的学习笔记。 使用 rqt_console 和 roslaunch 在两个终端里面分别运行： 123cd ~/catkin_ws/source ./devel/setup.bashrosrun rqt_console rqt_console 123cd ~/catkin_ws/source ./devel/setup.bashrosrun rqt_logger_level rqt_logger_level 会有如下窗口显示： 此时打开第三个终端，运行turtlesim： 123cd ~/catkin_ws/source ./devel/setup.bashrosrun turtlesim turtlesim_node 在rqt_logger_level里面设置日志等级为warn，再运行如下代码让乌龟撞墙，会看到rqt_console里面有日志打印。 123cd ~/catkin_ws/source ./devel/setup.bashrostopic pub /turtle1/cmd_vel geometry_m ...

本篇是对 ROS 官方 Tutorials “初级教程 1-7”部分的学习笔记。 安装和配置 ROS 环境 OS: Ubuntu 20.04.6 LTS ROS: Noetic Ninjemys 安装 123456789# 添加源sudo sh -c '. /etc/lsb-release && echo "deb http://mirrors.tuna.tsinghua.edu.cn/ros/ubuntu/ `lsb_release -cs` main" > /etc/apt/sources.list.d/ros-latest.list'# 添加密钥sudo apt-key adv --keyserver 'hkp://keyserver.ubuntu.com:80' --recv-key C1CF6E31E6BADE8868B172B4F42ED6FBAB17C654# 安装 rossudo apt updatesudo apt install ros-noetic-desktop-full 配置 ...

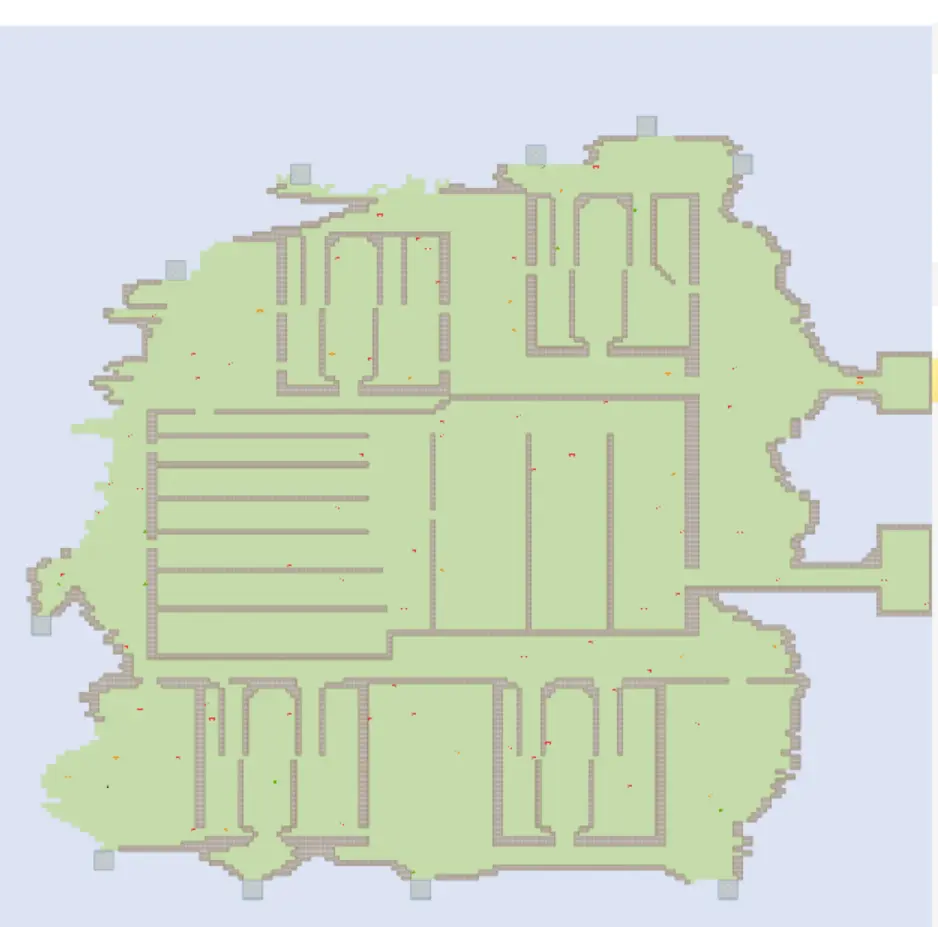
今年三月，受一起实习的好哥们邀请，参加了今年的华为软件精英挑战赛。已经多年没有参加比赛的我又一次体会了大学时候大家一起在实验室中攻克难关，互相帮助和鼓励的时光。说实话虽然很过度消耗精力，很累人，但是非常开心。 赛题介绍 赛题详细资料可以移步官方论坛查看。 我简单概括一下： 首先会有一张地图，地图是在程序初始化阶段由标准输入给出的，为 200*200 的字符矩阵，利用不同的字符，定义好海洋、陆地、泊位、障碍以及机器人等地图元素。 判题器会与竞赛软件通过标准输入输出做交互。首先传输初始化数据给竞赛软件，待竞赛软件初始化完成，反馈“OK”之后，评分正式开始进行。评分分周期进行，最多 15000 个周期，每个周期有 5ms 用作判题器处理，剩下时间给竞赛软件处理。理论上处理多久都可以，但 5min 时判题会结束，此时没有跑到的周期全部作废（处理不及时发生丢帧）。如果处理得快，win 和 mac 版本的判题器会有不同表现，win 版本判题器会等待到 15ms，再发下一帧数据；mac 版本的判题器会直接进入下个周期。 每个周期内，判题器会告知竞赛软件当前帧机器人以及船只的信息、帧数与分数、 ...

准备工作 vscode：官方网站 插件：vscode 中搜索插件 PlantUML 并进行安装，需要注意的是，如果使用 ssh 远程编辑，则还需在 remote 端安装此插件 graphviz：由于 PlantUML 是在 graphviz 基础上运行的，所以需要下载并安装 graphviz（下载页面）。如果不想本地安装，也有在线网页进行图形输出。 java环境：graphviz 的运行需要 java 环境，下载java。或者 linux 环境下直接 sudo apt install openjdk-17-jdk。 开始编辑 PlantUML 语法见官方手册 在任意一个文档（推荐新建后缀为.puml的文件）中输入 PlantUML 的代码，使用快捷键Alt+D（Macos 下可能是 Opt+D）即可实时预览自动排版的 UML 图。 效果如下（左边是代码，按了快捷键后自动分出右边窗口用来同步显示）： 常用技巧 分析类图 例如利用如下代码： 12345678910111213141516171819@startuml 分析类图boundary boundary_1control co ...

系列文章 《计算几何——算法与应用（第三版）》学习笔记1 - 扫描线（第1-4章） 《计算几何——算法与应用（第三版）》学习笔记2 - 空间索引（第5-7章） 番外篇 计算几何 - C++ 库的调研 Boost C++ Libraries学习 - Geometry -> Boost C++ Libraries学习 - Boost.Polygon (GTL) 参考 Boost 官方手册 The Boost.Polygon library provides algorithms focused on manipulating planar polygon geometry data. Specific algorithms provided are the polygon set operations (intersection, union, difference, disjoint-union) and related algorithms such as polygon connectivity graph extraction, offsetting and map-o ...

一般线性规划问题的数学模型 问题的提出 生产和经营管理中经常提出如何合理安排，使人力、物力等各种资源得到充分利用，获得最大的效益，这就是所谓线性规划问题。 问题提法千千万，总结起来都是：给定一定量的资源或任务，通过一种最优化的方案分配资源或任务，使得获得效益最大或者消耗资源最少。这时我们会有一个优化目标，以及其约束于（subject to, 或简写为 s.t.）的约束条件。 线性规划问题的数学模型 线性规划问题的数学模型包含三个组成要素： 决策变量：指决策者为实现规划目标采取的方案、措施，是问题中要确定的未知量。 目标函数：指问题要达到的目的要求，表示为决策变量的函数。 约束条件：指决策变量取值时受到的各种可用资源的限制，表示为含决策变量的等式或不等式。 如果在规划问题的数学模型中，决策变量为可控的连续变量，目标函数和约束条件都是线性的，这类模型称为线性规划问题的数学模型。一般写成如下形式： max(或min)z=CXmax(\text{或} min) z = CX max(或min)z=CX s.t.{AX≤(或=,≥)bX≥0s.t. \begin{cases} AX \ ...

系列文章 《计算几何——算法与应用（第三版）》学习笔记1 - 扫描线（第1-4章） -> 《计算几何——算法与应用（第三版）》学习笔记2 - 空间索引（第5-7章） 番外篇 计算几何 - C++ 库的调研 Boost C++ Libraries学习 - Geometry Boost C++ Libraries学习 - Boost.Polygon (GTL) 正交区域查找：数据库查询 将数据库中的每条记录对应到多维空间中的一个点，这样就可以将本来针对记录的查询变成针对点的查询。例如下图，把“yyyymmdd”格式的日期作为 x 坐标，把“月收入”作为 z 坐标，把“家庭成员数量”作为 y 坐标，图中的立方体就可以作为“查询出生于 1950 年至 1955 年之间、月收入在 $3000 至 $4000 之间并且家庭成员有 2 到 4 人的所有员工”的几何化表示。 有了这种表示，接下来要解决的问题是如何找到落在这个立方体中的点。在计算几何中，这类查询被称为矩形区域查询（rectangular range query），或者正交区域查找（orthogonal range query） ...