一般线性规划问题的数学模型
问题的提出
生产和经营管理中经常提出如何合理安排,使人力、物力等各种资源得到充分利用,获得最大的效益,这就是所谓线性规划问题。
问题提法千千万,总结起来都是:给定一定量的资源或任务,通过一种最优化的方案分配资源或任务,使得获得效益最大或者消耗资源最少。这时我们会有一个优化目标,以及其约束于(subject to, 或简写为 s.t.)的约束条件。
线性规划问题的数学模型
线性规划问题的数学模型包含三个组成要素:
- 决策变量:指决策者为实现规划目标采取的方案、措施,是问题中要确定的未知量。
- 目标函数:指问题要达到的目的要求,表示为决策变量的函数。
- 约束条件:指决策变量取值时受到的各种可用资源的限制,表示为含决策变量的等式或不等式。
如果在规划问题的数学模型中,决策变量为可控的连续变量,目标函数和约束条件都是线性的,这类模型称为线性规划问题的数学模型。一般写成如下形式:
max(或min)z=CX
s.t.{AX≤(或=,≥)bX≥0
A=⎣⎢⎢⎢⎡a11a21…am1a12a22…am2……⋱…a1na2n…amn⎦⎥⎥⎥⎤
线性规划问题的标准形式
max z=j=1∑ncjxj
s.t.{∑j=1naijxj=bixj≥0(i=1,…,m)
标准形式的线性规划模型中,目标函数为求极大值,约束条件全为等式,约束条件右端常数项 bi 全为非负值,变量 xj 的取值为非负。
如果某个线性规划问题不符合标准形式,也有方法转化成标准形式。
目标函数为求极小值
由于 min z⇔max (−z),只需令 z′=−z,有:
min z=j=1∑ncjxj⟹z′=−zmax z′=−j=1∑n(−cj)xj
约束条件为不等式
通过引入新的变量的形式,例如有约束条件为 2x1+2x2≤12,引入 x3≥0,观察等式两端,2x1+2x2 比右边小,需要加一个正数才有可能相等,于是将 x3 放在左边,变成 2x1+2x2+x3=12。同样的,10x1+12x2≥18 可以加入 x4≥0 变成 10x1+12x2=18+x4,适当移向即为标准形式中的表示:10x1+12x2−x4=18。
x3 称为松弛变量,x4 一般称为剩余变量,其现实意义是实际问题中未被充分利用的资源和超用的资源。
取值无约束的变量
当一个变量 x 在实际问题中没有 x≥0 的约束条件时,例如代表某产品当年计划数与上一年计划数之差,则其可以取任意值,不管是正、负还是 0。这时可令 x=x′−x′′,其中 x′≥0,x′′≥0,代回到线性规划模型即可。
变量取值小于或等于 0
当遇到某个变量取值范围为 xj≤0,可令 xj′=−xj,显然 xj′≥0。
线性规划问题的解
求解线性规划问题,就是从满足约束条件方程组的变量中找出一个解,使得目标函数取得最大值。
- 可行解:满足约束条件的解,全部可行解的集合称为可行域。
- 最优解:使目标函数达到最大值的可行解。
- 基:约束方程系数矩阵的满秩矩阵。基中每一个列向量称为基向量,与基向量对应的变量称为基变量。线性规划中除基变量以外的其他变量称为非基变量。
- 基解:令所有非基变量等于 0,则基变量有唯一解,加上前面取值为 0 的非基变量,就组成了线性规划问题的基解。
- 基可行解:满足变量非负约束条件的基解。
- 可行基:对应于基可行解的基。
图解法
步骤是:
- 建立坐标系,将约束条件在图上表示。
- 确立满足约束条件的解的范围。
- 绘制出目标函数的图形。
- 确定最优解。
例如,对于线性规划问题:
max z=2x1+3x2
s.t.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧2x1+2x24x15x2x1,x2≥0≤12≤16≤15
画出如下的区域:
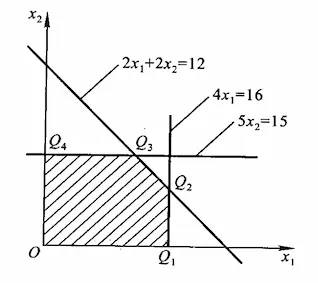
对于目标函数 z=2x1+3x2,z 是待定的值,我们将其化为 x2=−32x1+3z,易知其为平行于 x2=−32 的一族平行线。该平行线离原点越远则 z 的值越大,但事实上这条平行线不能移到无限远处,因为约束条件对 x1 和 x2 的值做了限定。
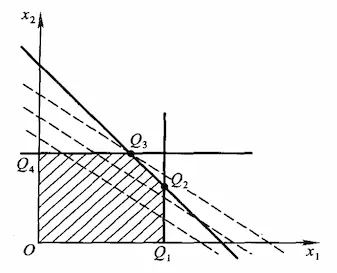
当平行线移动到 Q3 点上时,再继续移动就要脱离约束区域了,所以该点处取得最优解,将 Q3 对应的 x1 和 x2 值代入目标函数则可以求得最优解。
无穷多最优解
有时候寻找距离远点最远的直线过程中,会发现最后直线与约束区域相交的不是一个点,而是一条线,这时线上的任意点都使目标函数值 z 达到最大,即该线性规划问题有无穷多最优解,也称具有多重最优解。
无界解(或无最优解)
如果约束区域不是一个封闭的图形,则有可能直线可以移动到无穷远处,这种情况下称问题具有无界解或无最优解。其原因是在建立实际问题的数学模型时遗漏了某些必要的资源约束。
无可行解
如果用图解法找不到满足所有约束条件的公共范围,这时问题无可行解。其原因是模型本身有错误,约束条件之间相互矛盾,应检查修正。
总结
- 求解线性规划问题时,解的情况有:唯一最优解、无用多最优解、无界解、无可行解;
- 若线性规划问题的可行域存在,则可行域是一个凸集;
- 若线性规划问题的最优解存在,则最优解或最优解之一(如果有无穷多的话)一定能够在可行域(凸集)的某个顶点找到;
- 解题思路是,线找出凸集的任一顶点,计算在顶点处的目标函数值。比较周围相邻顶点的目标函数值是否比这个值更优,如果为否,则该顶点就是最优解的点或最优解的点之一,否则转到比这个点的目标函数值更优的另一顶点,重复上述过程,直到找出使目标函数值达到最优的顶点为止。
单纯形法原理
1947 年由 G. B. Dantzig 提出。
凸集和顶点
凸集:如果集合 C 中任意两个点 X1、X2,其连线上的所有点也都是集合 C 中的点,称 C 为凸集。
由于 X1、X2 的连线可表示为 aX1+(1−a)X2 (0<a<1),凸集的定义可表示为:
对任何 X1∈C, X2∈C,有 aX1+(1−a)X2∈C (0<a<1),则称 C 为凸集。
顶点:凸集 C 中满足下述条件的点 X 称为顶点:如果 C 中不存在任何两个不同的点 X1、X2,使 X 成为这两个点连线上的一个点,或者说对任何 X1∈C, X2∈C,不存在 X=aX1+(1−a)X2 (0<a<1),则称 X 是凸集的顶点。
几个基本定理的证明
定理 1
若线性规划问题存在可行解,则问题的可行域是凸集。
引理:线性规划问题的可行解 X=(x1,…,xn)T 为基可行解的充要条件是 X 的正分量所对应的系数列向量是线性独立的。
定理 2
线新规划问题的基可行解 X 对应线性规划问题可行域(凸集)的顶点。
定理 3
若线性规划问题有最优解,一定存在一个基可行解是最优解。
确定初始基可行解
单纯形法的基本思路:线找到一个初始基可行解,如果不是最优解,设法转换到另一个基可行解,并使目标函数值不断增大,一直到找到最优解为止。
给定线性规划问题:
max z=j=1∑ncjxj
s.t.{∑j=1naijxj≤bixj≥0(i=1,…,m)(j=1,…,n)
在第 i 个约束条件上加上松弛变量 xsi(i=1,…,m),化为标准形式:
max z=j=1∑ncjxj+0i=1∑mxsi
s.t.{∑j=1naijxj+xsi=bixj≥0(i=1,…,m)(j=1,…,n)
其约束方程组的系数矩阵为:
⎣⎢⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2………a1na2n⋮amn10⋮001⋮0………00⋮1⎦⎥⎥⎥⎥⎤
由于系数矩阵中含有一个单位矩阵 (Ps1,…,Psm),只要以这个单位矩阵作为基,既可以立即解出变量值 xsi=bi(i=1,…,m)。因为 bi≥0(i=1,…,m),因此 X=(0,…,0,b1,…,bm)T 就是一个基可行解。
特殊地,当线性规划约束条件为 = 或 ≥ 时,化为标准形式也一般不包含单位矩阵,这时可以通过人工添加变量来构造一个单位矩阵作为基,称作人工基。
从初始基可行解转换为另一基可行解
初始基可行解为 X(0)=(x10,…,xn0)T,其中非零坐标有 m 个,位置任意。假设前 m 个坐标就是非零坐标,即 X(0)=(x10,…,xm0,0,…,0)T。
由于 X(0)∈C,有 ∑i=1nPixi0=b。其增广矩阵(包括用人工基的方法,总可以写成单位矩阵形式)为:
⎣⎢⎢⎢⎢⎡10⋮001⋮0………00⋮1a1,m+1a2,m+1⋮am,m+1………a1ja2j⋮amj………a1na2n⋮amnb1b2⋮bm⎦⎥⎥⎥⎥⎤
由于 P1,…,Pm 是一个基,其他向量 Pj 可用这个基的线性组合来表示,有:
Pj=i=1∑maijPi⇔Pj−i=1∑maijPi=0
θ(Pj−i=1∑maijPi)=0
将其代回到 ∑i=1nPixi0=b,有
i=1∑n(xi0−θaij)Pi+θPj=b
知 X(1)=(x10−θa1j,…,xm0−θamj,0,…,θ,…,0) 是约束方程组上的另一个点,其中 θ 是 X(1) 的第 j 个坐标的值。
由于 θ>0,要使得 X(1) 是一个基可行解,应有 xi0−θaij≥0 (i=1,…,m),且由于当 aij≤0 时,该式显然成立,所以 m 个不等式至少有一个等号成立。
令:
θ=imin{aijxi0∣aij>0}=aijxi0
有:
xi0−θa{=0≥0(i=l)(i=l)
这样 X(1) 中的正的分量最多有 m 个,容易证明 m 个向量 P1,…,Pl−1,Pl+1,…,Pm,Pj 线性无关,以这个方法确定的 θ 值,能使得 X(1) 是一个新的基可行解。
最优性检验和解的判别
将基可行解 X(0) 和 X(1) 分别代入目标函数,得:
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧z(0)z(1)=∑i=1mcixi0=∑i=1mci(xi0−θaij)+θc=∑i=1mcixi0+θ(cj−∑i=1mciaij)=z(0)+θ(cj−∑i=1mciaij)
由于 θ>0,所以只要 (cj−∑i=1mciaij)>0,就有 z(1)>z(0),通常令 σj=(cj−zj)=(cj−∑i=1mciaij),满足:
- 当所有的 σj≤0 时,表明现有顶点(基可行解)的目标函数值比起相邻各顶点(基可行解)的目标函数都大,现有顶点对应的基可行解即为最优解。
- 当所有的 σj≤0,又对某个非基变量 xj 有 cj−zj=0,且按照上面说的 θ 寻找方法可以找到 θ>0,这表明可以找到另一顶点(基可行解)目标函数值也达到最大。由于该两点连线上的点也属于可行域内的点,且目标函数值相等,即该线性规划问题有无穷多最优解。
- 如果存在某个 σj>0,又 Pj 向量的所有分量 aij≤0,又由于对任意 θ>0,恒有 xi0−θaij≥0。因 θ 取值可无限增大,所以目标函数也可以无限增大,这时线性规划问题存在无界解。
单纯形法的计算步骤
- 求出线性规划的初始基可行解。
为了计算上的方便和规格化,对单纯形法计算设计了一种专门表格,称为单纯形表。
- 进行最优性检验。
- 从一个基可行解转换到另一个目标函数值更大的基可行解,列出新的单纯形表。
- 重复第二、三步直到计算终止。