《运筹学基础及应用（第五版）》学习笔记 - 线性规划

一般线性规划问题的数学模型

问题的提出

生产和经营管理中经常提出如何合理安排，使人力、物力等各种资源得到充分利用，获得最大的效益，这就是所谓线性规划问题。

问题提法千千万，总结起来都是：给定一定量的资源或任务，通过一种最优化的方案分配资源或任务，使得获得效益最大或者消耗资源最少。这时我们会有一个优化目标，以及其约束于（subject to, 或简写为 s.t.）的约束条件。

线性规划问题的数学模型

线性规划问题的数学模型包含三个组成要素：

决策变量：指决策者为实现规划目标采取的方案、措施，是问题中要确定的未知量。
目标函数：指问题要达到的目的要求，表示为决策变量的函数。
约束条件：指决策变量取值时受到的各种可用资源的限制，表示为含决策变量的等式或不等式。

如果在规划问题的数学模型中，决策变量为可控的连续变量，目标函数和约束条件都是线性的，这类模型称为线性规划问题的数学模型。一般写成如下形式：

max(\text{或} min) z = CX

s.t. \begin{cases} AX \le (\text{或} =, \ge) b \\ X \ge 0 \end{cases}

A = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \dots & \dots & \ddots & \dots \\ a_{m1} & a_{m2} & \dots & a_{mn} \\ \end{bmatrix}

线性规划问题的标准形式

max\ z = \sum_{j=1}^n c_j x_j

s.t. \begin{cases} \sum_{j=1}^n a_{ij} x_j = b_i & (i = 1, \dots, m) \\ x_j \ge 0 \end{cases}

标准形式的线性规划模型中，目标函数为求极大值，约束条件全为等式，约束条件右端常数项 $b_i$ 全为非负值，变量 $x_j$ 的取值为非负。

如果某个线性规划问题不符合标准形式，也有方法转化成标准形式。

目标函数为求极小值

由于 $min \ z \Leftrightarrow max \ (-z)$ ，只需令 $z' = -z$ ，有：

min \ z = \sum_{j=1}^n c_j x_j \stackrel{z'=-z}{\Longrightarrow} max \ z' = -\sum_{j=1}^n (-c_j)x_j

约束条件为不等式

通过引入新的变量的形式，例如有约束条件为 $2x_1+2x_2\le12$ ，引入 $x_3\ge0$ ，观察等式两端， $2x_1+2x_2$ 比右边小，需要加一个正数才有可能相等，于是将 $x3$ 放在左边，变成 $2x_1+2x_2+x_3=12$ 。同样的， $10x_1+12x_2\ge18$ 可以加入 $x_4\ge0$ 变成 $10x_1+12x_2=18+x_4$ ，适当移向即为标准形式中的表示： $10x_1+12x_2-x_4=18$ 。

$x_3$ 称为松弛变量， $x_4$ 一般称为剩余变量，其现实意义是实际问题中未被充分利用的资源和超用的资源。

取值无约束的变量

当一个变量 $x$ 在实际问题中没有 $x\ge0$ 的约束条件时，例如代表某产品当年计划数与上一年计划数之差，则其可以取任意值，不管是正、负还是 $0$ 。这时可令 $x=x'-x''$ ，其中 $x'\ge0, x''\ge0$ ，代回到线性规划模型即可。

变量取值小于或等于 0

当遇到某个变量取值范围为 $x_j\le0$ ，可令 $x_j'=-x_j$ ，显然 $x_j'\ge0$ 。

线性规划问题的解

求解线性规划问题，就是从满足约束条件方程组的变量中找出一个解，使得目标函数取得最大值。

可行解：满足约束条件的解，全部可行解的集合称为可行域。
最优解：使目标函数达到最大值的可行解。
基：约束方程系数矩阵的满秩矩阵。基中每一个列向量称为基向量，与基向量对应的变量称为基变量。线性规划中除基变量以外的其他变量称为非基变量。
基解：令所有非基变量等于 $0$ ，则基变量有唯一解，加上前面取值为 $0$ 的非基变量，就组成了线性规划问题的基解。
基可行解：满足变量非负约束条件的基解。
可行基：对应于基可行解的基。

图解法

步骤是：

建立坐标系，将约束条件在图上表示。
确立满足约束条件的解的范围。
绘制出目标函数的图形。
确定最优解。

例如，对于线性规划问题：

max\ z = 2x_1+3x_2

s.t. \begin{cases} 2x_1+2x_2 &\le12 \\ 4x_1 &\le16 \\ 5x_2 &\le15 \\ x_1, x_2 \ge0 \end{cases}

画出如下的区域：

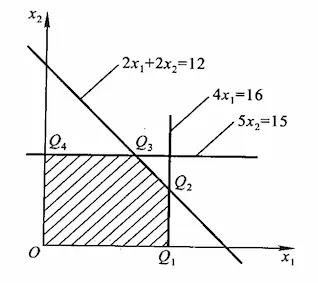
对于目标函数 $z = 2x_1+3x_2$ ， $z$ 是待定的值，我们将其化为 $x_2 = -{2 \over 3} x_1 + {z \over 3}$ ，易知其为平行于 $x_2 = -{2 \over 3}$ 的一族平行线。该平行线离原点越远则 $z$ 的值越大，但事实上这条平行线不能移到无限远处，因为约束条件对 $x_1$ 和 $x_2$ 的值做了限定。

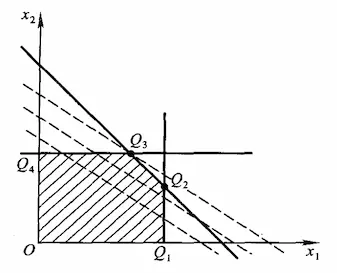
当平行线移动到 $Q_3$ 点上时，再继续移动就要脱离约束区域了，所以该点处取得最优解，将 $Q_3$ 对应的 $x_1$ 和 $x_2$ 值代入目标函数则可以求得最优解。

无穷多最优解

有时候寻找距离远点最远的直线过程中，会发现最后直线与约束区域相交的不是一个点，而是一条线，这时线上的任意点都使目标函数值 $z$ 达到最大，即该线性规划问题有无穷多最优解，也称具有多重最优解。

无界解（或无最优解）

如果约束区域不是一个封闭的图形，则有可能直线可以移动到无穷远处，这种情况下称问题具有无界解或无最优解。其原因是在建立实际问题的数学模型时遗漏了某些必要的资源约束。

无可行解

如果用图解法找不到满足所有约束条件的公共范围，这时问题无可行解。其原因是模型本身有错误，约束条件之间相互矛盾，应检查修正。

总结

求解线性规划问题时，解的情况有：唯一最优解、无用多最优解、无界解、无可行解；
若线性规划问题的可行域存在，则可行域是一个凸集；
若线性规划问题的最优解存在，则最优解或最优解之一（如果有无穷多的话）一定能够在可行域（凸集）的某个顶点找到；
解题思路是，线找出凸集的任一顶点，计算在顶点处的目标函数值。比较周围相邻顶点的目标函数值是否比这个值更优，如果为否，则该顶点就是最优解的点或最优解的点之一，否则转到比这个点的目标函数值更优的另一顶点，重复上述过程，直到找出使目标函数值达到最优的顶点为止。

单纯形法原理

1947 年由 G. B. Dantzig 提出。

凸集和顶点

凸集：如果集合 $C$ 中任意两个点 $X_1$ 、 $X_2$ ，其连线上的所有点也都是集合 $C$ 中的点，称 $C$ 为凸集。
由于 $X_1$ 、 $X_2$ 的连线可表示为 $aX_1 + (1-a)X_2\ (0<a<1)$ ，凸集的定义可表示为：

对任何 $X_1 \in C,\ X_2 \in C$ ，有 $aX_1 + (1-a)X_2 \in C\ (0<a<1)$ ，则称 $C$ 为凸集。

顶点：凸集 $C$ 中满足下述条件的点 $X$ 称为顶点：如果 $C$ 中不存在任何两个不同的点 $X_1$ 、 $X_2$ ，使 $X$ 成为这两个点连线上的一个点，或者说对任何 $X_1 \in C,\ X_2 \in C$ ，不存在 $X = a X_1 + (1-a)X_2 \ (0<a<1)$ ，则称 $X$ 是凸集的顶点。

几个基本定理的证明

TODO: 详细证明过程

定理 1

若线性规划问题存在可行解，则问题的可行域是凸集。

引理：线性规划问题的可行解 $X=(x_1, \dots, x_n)^T$ 为基可行解的充要条件是 $X$ 的正分量所对应的系数列向量是线性独立的。

定理 2

线新规划问题的基可行解 $X$ 对应线性规划问题可行域（凸集）的顶点。

定理 3

若线性规划问题有最优解，一定存在一个基可行解是最优解。

确定初始基可行解

单纯形法的基本思路：线找到一个初始基可行解，如果不是最优解，设法转换到另一个基可行解，并使目标函数值不断增大，一直到找到最优解为止。

给定线性规划问题：

max\ z = \sum_{j=1}^n c_j x_j

s.t. \begin{cases} \sum_{j=1}^n a_{ij} x_j \le b_i & (i = 1, \dots, m) \\ x_j \ge 0 & (j=1,\dots,n) \end{cases}

在第 $i$ 个约束条件上加上松弛变量 $x_{si}(i=1,\dots,m)$ ，化为标准形式：

max\ z = \sum_{j=1}^n c_j x_j + 0\sum_{i=1}^m x_{si}

s.t. \begin{cases} \sum_{j=1}^n a_{ij} x_j + x_{si} = b_i & (i = 1, \dots, m) \\ x_j \ge 0 & (j=1,\dots,n) \end{cases}

其约束方程组的系数矩阵为：

\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} & 1 & 0 & \dots & 0 \cr a_{21} & a_{22} & \dots & a_{2n} & 0 & 1 & \dots & 0 \cr \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots \cr a_{m1} & a_{m2} & \dots & a_{mn} & 0 & 0 & \dots & 1 \end{bmatrix}

由于系数矩阵中含有一个单位矩阵 $(P_{s1},\dots,P_{sm})$ ，只要以这个单位矩阵作为基，既可以立即解出变量值 $x_{si}=b_i(i=1,\dots,m)$ 。因为 $b_i\ge0 (i=1,\dots,m)$ ，因此 $X=(0,\dots,0,b_1,\dots,b_m)^T$ 就是一个基可行解。

特殊地，当线性规划约束条件为 $=$ 或 $\ge$ 时，化为标准形式也一般不包含单位矩阵，这时可以通过人工添加变量来构造一个单位矩阵作为基，称作人工基。

从初始基可行解转换为另一基可行解

初始基可行解为 $X^{(0)}=(x_1^0,\dots,x_n^0)^T$ ，其中非零坐标有 $m$ 个，位置任意。假设前 $m$ 个坐标就是非零坐标，即 $X^{(0)}=(x_1^0,\dots,x_m^0,0,\dots,0)^T$ 。
由于 $X^{(0)} \in C$ ，有 $\sum_{i=1}^n P_i x_i^0 = b$ 。其增广矩阵（包括用人工基的方法，总可以写成单位矩阵形式）为：

\left[ \begin{array}{ccccccccc|c} 1 & 0 & \dots & 0 & a_{1,m+1} & \dots & a_{1j} & \dots & a_{1n} & b_1 \cr 0 & 1 & \dots & 0 & a_{2,m+1} & \dots & a_{2j} & \dots & a_{2n} & b_2 \cr \vdots & \vdots && \vdots & \vdots && \vdots && \vdots & \vdots \cr 0 & 0 & \dots & 1 & a_{m,m+1} & \dots & a_{mj} & \dots & a_{mn} & b_m \cr \end{array} \right]

由于 $P_1,\dots,P_m$ 是一个基，其他向量 $P_j$ 可用这个基的线性组合来表示，有：

P_j = \sum_{i=1}^m a_{ij} P_i \Leftrightarrow P_j - \sum_{i=1}^m a_{ij} P_i = 0

\theta (P_j - \sum_{i=1}^m a_{ij} P_i) = 0

将其代回到 $\sum_{i=1}^n P_i x_i^0 = b$ ，有

\sum_{i=1}^n (x_i^0 - \theta a_{ij})P_i + \theta P_j = b

知 $X^{(1)} = (x_1^0-\theta a_{1j},\dots,x_m^0-\theta a_{mj},0,\dots,\theta,\dots,0)$ 是约束方程组上的另一个点，其中 $\theta$ 是 $X^{(1)}$ 的第 $j$ 个坐标的值。

由于 $\theta > 0$ ，要使得 $X^{(1)}$ 是一个基可行解，应有 $x_i^0-\theta a_{ij} \ge 0\ (i=1,\dots,m)$ ，且由于当 $a_{ij} \le 0$ 时，该式显然成立，所以 $m$ 个不等式至少有一个等号成立。

令：

\theta=\min_i\{ {x_i^0 \over a_{ij}} \mid a_{ij} > 0 \} = {x_i^0 \over a_{ij}}

有：

x_i^0-\theta a \begin{cases} =0 & (i=l) \cr \ge0 & (i \ne l) \end{cases}

这样 $X^{(1)}$ 中的正的分量最多有 $m$ 个，容易证明 $m$ 个向量 $P_1,\dots,P_{l-1},P_{l+1},\dots,P_m,P_j$ 线性无关，以这个方法确定的 $\theta$ 值，能使得 $X^{(1)}$ 是一个新的基可行解。

最优性检验和解的判别

将基可行解 $X^{(0)}$ 和 $X^{(1)}$ 分别代入目标函数，得：

\begin{cases} z^{(0)} &= \sum_{i=1}^m c_i x_i^0 \cr z^{(1)} &= \sum_{i=1}^m c_i (x_i^0 - \theta a_{ij}) + \theta c \cr &= \sum_{i=1}^m c_i x_i^0 + \theta(c_j - \sum_{i=1}^m c_i a_{ij}) \cr &= z^{(0)} + \theta(c_j - \sum_{i=1}^m c_i a_{ij}) \end{cases}

由于 $\theta > 0$ ，所以只要 $(c_j - \sum_{i=1}^m c_i a_{ij}) > 0$ ，就有 $z^{(1)} > z^{(0)}$ ，通常令 $\sigma_j = (c_j - z_j) = (c_j - \sum_{i=1}^m c_i a_{ij})$ ，满足：

当所有的 $\sigma_j \le 0$ 时，表明现有顶点（基可行解）的目标函数值比起相邻各顶点（基可行解）的目标函数都大，现有顶点对应的基可行解即为最优解。
当所有的 $\sigma_j \le 0$ ，又对某个非基变量 $x_j$ 有 $c_j-z_j=0$ ，且按照上面说的 $\theta$ 寻找方法可以找到 $\theta>0$ ，这表明可以找到另一顶点（基可行解）目标函数值也达到最大。由于该两点连线上的点也属于可行域内的点，且目标函数值相等，即该线性规划问题有无穷多最优解。
如果存在某个 $\sigma_j>0$ ，又 $P_j$ 向量的所有分量 $a_{ij}\le0$ ，又由于对任意 $\theta>0$ ，恒有 $x_i^0-\theta a_{ij}\ge0$ 。因 $\theta$ 取值可无限增大，所以目标函数也可以无限增大，这时线性规划问题存在无界解。