学习pygame的过程中,照着自己对2048游戏的理解,写了自己版本的2048游戏。于是自然地想是否能写一些算法让程序自动解2048呢?经过一番学习发现了Min-Max算法,令人高兴的是这个算法泛用性极佳,可以解决一大类的博弈问题。
游戏实现
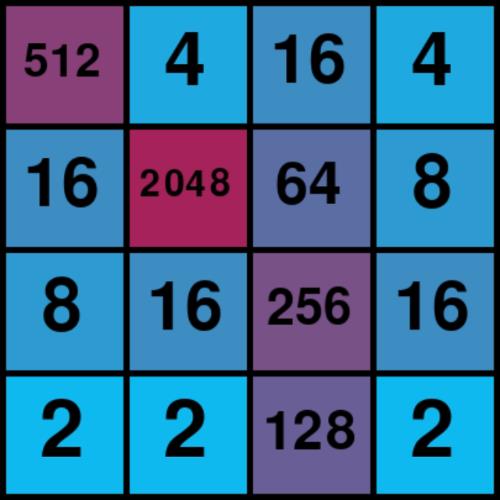
2048游戏本体其实非常简单,只需要维护一个矩阵,实现矩阵的一个方向移动,其他方向的移动可以全部转换成已经实现的这一种移动就好了。使用pygame来显示这个矩阵,就完成了游戏程序。
卡片移动
这里我选择只实现左移操作。右移操作可以通过矩阵水平翻转变成左移操作,左移完再水平翻转回来;上移操作可以通过逆时针旋转90°转换为左移操作,左移完再顺时针旋转回来;下移操作同理。
左移的原理是:
去掉每一行中的所有0,这个操作会让所有非0的元素相互紧贴。
遍历剩余的每一行元素,将相邻的相同元素变为前一个是原本的两倍,后一个变为0。这个操作会将应当合并的数合并。
再次去掉剩余元素中因为步骤2带来的0元素,使得元素紧贴。
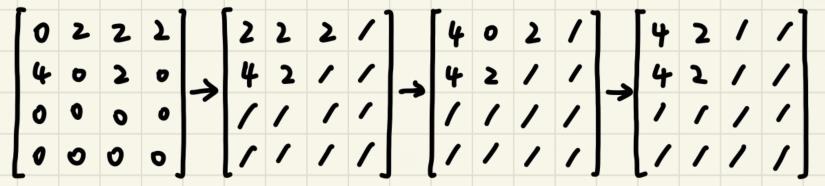
最后在末尾补齐0,让矩阵回到原本的大小,就完成了一次移动。
过程举例如图:
Game.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class Game2048 : def step (self, direction, animate=True ): cards_to_move = copy.deepcopy(self.card_numbers) cards_to_compare = copy.deepcopy(self.card_numbers) if direction == RIGHT: cards_to_move = np.flip(self.card_numbers, axis=1 ) elif direction == DOWN: cards_to_move = np.rot90(self.card_numbers, -1 ) elif direction == UP: cards_to_move = np.rot90(self.card_numbers, 1 ) row_length = cards_to_move.shape[0 ] cards_to_move = [[n for n in row if n != 0 ] for row in cards_to_move] for row in cards_to_move: for i in range (1 , len (row)): if row[i] == row[i-1 ]: row[i-1 ] *= 2 row[i] = 0 cards_to_move = [[n for n in row if n != 0 ] for row in cards_to_move] for i in range (len (cards_to_move)): current_row_length = len (cards_to_move[i]) cards_to_move[i] = np.hstack((cards_to_move[i], np.zeros(row_length-current_row_length))) cards_to_move = np.array(cards_to_move, dtype=int ) if direction == RIGHT: cards_to_move = np.flip(cards_to_move, axis=1 ) elif direction == DOWN: cards_to_move = np.rot90(cards_to_move, 1 ) elif direction == UP: cards_to_move = np.rot90(cards_to_move, -1 ) self.card_numbers = cards_to_move if animate: pass if False in operator.eq(cards_to_move, cards_to_compare): self.generate(2 ) return True return False
随机生成卡片
随机生成卡片的功能需要用到我们的老朋友:洗牌算法。幸运的是np模块已经帮我们实现了洗牌算法。我们只需将所有数字为0的坐标记录下来,加入到列表里面,洗牌该列表并取出第一个坐标,生成数字。Game.py
1 2 3 4 5 6 class Game2048 : def generate (self, number ): empty_positions = [(i, j) for i in range (BOARDRIGHT) for j in range (BOARDBOTTOM) if self.card_numbers[i][j] == 0 ] if len (empty_positions) > 0 : np.random.shuffle(empty_positions) self.card_numbers[empty_positions[0 ][0 ]][empty_positions[0 ][1 ]] = number
pygame相关
游戏GUI部分,我们会维护一个包含很多pygame.Rect的二维list,这些矩形的位置是一直不变的,移动的动画通过“新建一个方块,完成移动动画,再删除该方块”完成(下面的版本没有放出这段代码,因为我觉得这个实现方式不够优雅)。每一帧我们会计算矩阵的颜色以及上面需要显示的数字。
Game.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 import copyimport operatorimport pygameimport sysimport numpy as npRECTSIZE = 100 GAPSIZE = 5 IDLE = 0 UP = 1 DOWN = 2 LEFT = 3 RIGHT = 4 DIRECTIONS = (UP, DOWN, LEFT, RIGHT) DIRECTIONNAMES = ('IDLE' , 'UP' , 'DOWN' , 'LEFT' , 'RIGHT' ) BOARDSIZE = BOARDRIGHT, BOARDBOTTOM = 4 , 4 STARTCARDAMOUNT = 4 STARTCARDNUMBER = 2 SCREEN_X = RECTSIZE * BOARDRIGHT + GAPSIZE SCREEN_Y = RECTSIZE * BOARDBOTTOM + GAPSIZE COLOR_BACK = (0 , 0 , 0 ) COLOR_CELL = (200 , 200 , 200 ) fps = 60 MOVE_SPEED = 60 def show_text (screen, pos, text, color, font_size = RECTSIZE, font_bold = False , font_italic = False ): cur_font = pygame.font.Font(None , font_size) cur_font.set_bold(font_bold) cur_font.set_italic(font_italic) text_fmt = cur_font.render(text, 1 , color) screen.blit(text_fmt, text_fmt.get_rect(center=(pos[0 ] + (RECTSIZE-GAPSIZE*2 )//2 , pos[1 ] + (RECTSIZE-GAPSIZE*2 )//2 ))) class Game2048 : def __init__ (self, allow_input = True ): self.game_over = False self.recv_input = allow_input pygame.init() screen_size = SCREEN_X, SCREEN_Y self.screen = pygame.display.set_mode(screen_size) pygame.display.set_caption("2048" ) self.clock = pygame.time.Clock() self.rectangles = [[pygame.Rect(i * RECTSIZE + GAPSIZE, j * RECTSIZE + GAPSIZE, RECTSIZE - GAPSIZE, RECTSIZE - GAPSIZE) for i in range (BOARDRIGHT)] for j in range (BOARDBOTTOM)] self.card_numbers = np.array([[0 for _ in range (BOARDRIGHT)] for _ in range (BOARDBOTTOM)], dtype=int ) self.generate(2 ) self.generate(2 ) def init (self ): pass def getcards (self ): return self.card_numbers def setcards (self, numbers ): self.card_numbers = copy.deepcopy(numbers) def setnumber (self, x, y, number ): self.card_numbers[x][y] = number def step (self, direction, animate=True ): pass def generate (self, number ): pass def routine (self ): for event in pygame.event.get(): if event.type == pygame.QUIT: self.game_over = True sys.exit() if self.recv_input and event.type == pygame.KEYDOWN: if event.key == pygame.K_w: self.step(UP) elif event.key == pygame.K_s: self.step(DOWN) elif event.key == pygame.K_a: self.step(LEFT) elif event.key == pygame.K_d: self.step(RIGHT) self.screen.fill(COLOR_BACK) self.display() pygame.display.update() self.clock.tick(fps) def display (self ): for i in range (BOARDRIGHT): for j in range (BOARDBOTTOM): number = self.card_numbers[i][j] level = int (np.log2(number)) if number != 0 else 0 color = (level*15 , 200 - level*15 , 255 - level*15 ) if level != 0 else COLOR_CELL rect = self.rectangles[i][j] pygame.draw.rect(self.screen, color, rect, 0 ) if number != 0 : rectpos = (rect.x, rect.y) show_text(self.screen, rectpos, str (number), COLOR_BACK, RECTSIZE - level*5 )
Min-Max
对于完全信息、零和博弈的游戏,假设“对方”是一个“聪明”的选手,总会做出使“我方”收益最低的决策。对于此“收益”,我们需要一个评估函数来给当前的场面评分。
在“我方”行动的回合,总会寻找令场面评分最高 的行动方式,称为max层。
在“对方”行动的回合,总会寻找令场面评分最低 的行动方式,成为min层。
可以这么理解:评估函数对场面的评分代表着此时局面对我方的有利程度,所以场面评分越高越好(场面评分对于我方越高时,意味着局面对于对方来说越失利)。那么,我们可以做很粗暴的一件事情:我们把当前我们可以进行的行为全部模拟进行一遍,然后对于这其中的每一种情况,执行完之后就应该轮到对方了,我们也将对方可以进行的行为全部模拟进行一遍,直到到达我们设定的搜索深度。之后我们计算当前的场面评估值,再利用Min-Max的规则回溯到根节点,根节点找到会达到最大评估值的分支,而这个分支对应一个目前能进行的操作。
在这样的思想下,很明显我们不太可能达到令场面值取最大值的情况,因为那种情况会被min节点给避免掉,我们只能达到一种“在最坏情况下的最好场面”,所以说Min-Max算法是悲观算法。
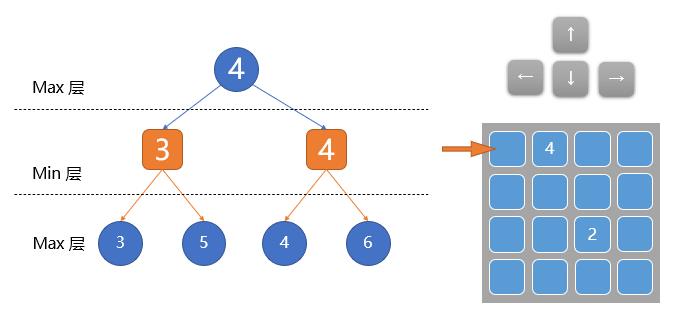
对于2048游戏来说,max层可以进行的操作是上下左右四个移动方向(如下图右上),min层可以进行的操作是往所有空格的地方填上数字(如下图右下)。
Min-Max规则举例来说:
可以看到每一个max层我们都会获得其所有子树中值最大的数,而所有min层中我们会获得所有子树中值最小的数。那为什么既然我们都知道要走min层的4那个分支了,还要搜索第二个max层的前面两个节点呢?这是因为这里所有的“值”不是当前的局面的评估值,而是搜索到最深时那时候的局面造成的评估值。
Alpha-Beta剪枝优化
因为我们的搜索是深度优先的,所以在搜索其他路径时,其实我们已经知道了一些结果,如果我们发现当前路径会出现一个对自己非常不利的场面值,那由于悲观算法的特性,我们会认为min节点一定会引导我们通向那个场面,所以这个路径没有继续搜索下去的必要了,于是剪掉该节点继续搜索下去的其他情况,回溯到上一个节点继续搜索。
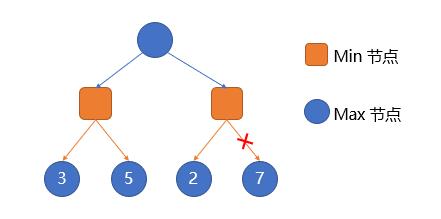
举例来说:
当搜索到右边的min节点时,我们已经知道左边的min节点会是3,此时我们搜索子树,发现第一个子树的值是2,此时不管后面的子树值是多少,如果我们在该min节点填2,上面的max节点也肯定会选值为3的节点而不是当前这个至多是2的节点,所以进行剪枝,该节点未搜索的所有子树均不需要计算了。
以上的例子让我们对Alpha-Beta剪枝算法有了一个较为直观的理解,那么具体应该怎么操作呢?我也还是先用我通俗的语言解释为什么该这么做吧,更加具体的相信读了我的解释之后再去看代码会很容易懂。
通过之前的分析我们知道,在处理min节点时,我们得知道其兄弟节点是否已经有较大的值了,因为如果有的话,这个min节点的父节点作为max节点是一定会选择那个分支而不会选择这个分支,这时候就没有继续搜索下去的必要了。这个值怎么来呢?很容易想到应该由这个min节点的父max节点来维护,父max节点每完成一个操作,就会调用beta函数去模拟min节点的操作。所以父max节点维护所有已经搜索过的beta分支的返回值,取其最大值作为下一次调用beta函数时的alpha值传下去。
MinMax.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 class MinMax : def solve (self, params, depth ): val, direction = self.alpha(params, depth) return direction def alpha (self, params, max_depth, current_depth=1 , alpha_val=-np.inf, beta_val=np.inf ): if current_depth >= max_depth: return self.evaluate(params), Game.IDLE max_val = alpha_val max_dir = Game.IDLE current_numbers = copy.deepcopy(self.get_numbers()) for direction in Game.DIRECTIONS: self.game.setcards(current_numbers) if self.game.step(direction, False ): new_beta_val = self.beta(params, max_depth, current_depth+1 , max_val, beta_val) if new_beta_val > max_val: max_val = new_beta_val max_dir = direction if max_val >= beta_val: return max_val, max_dir return max_val, max_dir def beta (self, params, max_depth, current_depth=1 , alpha_val=-np.inf, beta_val=np.inf ): if current_depth >= max_depth: return self.evaluate(params) min_val = beta_val current_numbers = copy.deepcopy(self.get_numbers()) for i in range (current_numbers.shape[0 ]): for j in range (current_numbers.shape[1 ]): if current_numbers[i][j] == 0 : self.game.setcards(current_numbers) self.game.setnumber(i, j, 2 ) new_alpha_val, _ = self.alpha(params, max_depth, current_depth+1 , alpha_val, min_val) if new_alpha_val < min_val: min_val = new_alpha_val if alpha_val >= min_val: return min_val return min_val
评估函数
Min-Max算法在搜索的过程中除了引入了博弈双方可以如何进行操作之外,没有引入游戏规则相关的东西。那么如何使用Min-Max算法让程序的搜索能够引导走向胜利呢,这就需要评估函数的参与了。评估函数和游戏规则非常相关,可以说评估函数的编写与算法的表现强相关。
对于2048游戏来说,凭我的经验,我认为局面应当足够“整齐”,也就是说接下来如果有新的卡片来了,我们需要一级一级合并上去的时候,不会出现那种明明有两个卡片可以合并,但因为它们中间隔着一个其他卡片的情况。所以我觉得棋局的排布应该“平滑”,而且应该“单调”。同时,我们应该尽可能地合并卡片,所以卡片数量越少越好,也就是“空格数”越大越好,“重复数”越少越好,“平均数”越大越好。当然,我们也应该关注棋局上“最大值”,毕竟这才是我们的终极目标。
平滑度
判断平滑度,我的方法是将奇数行倒过来,再把矩阵展平,计算相邻数字的差值,并将这些差值求和。
MinMax.py
1 2 3 4 5 6 7 8 9 10 class MinMax : def smooth (self, card_numbers, card_levels ): unfolded_cards = [row if idx%2 == 0 else row[::-1 ] for idx, row in enumerate (card_levels)] flatten_cards = np.array(unfolded_cards).flatten() for i in range (1 , len (flatten_cards)): flatten_cards[i-1 ] = flatten_cards[i]-flatten_cards[i-1 ] return -np.sum (flatten_cards[:-1 ])
单调性
单调性的判断方法和平滑性差不多,也是“蛇形”判断,给逆序的情况以惩罚。
1 2 3 4 5 6 7 8 9 10 11 class MinMax : def mono (self, card_numbers, card_levels ): unfolded_cards = [row if idx%2 == 0 else row[::-1 ] for idx, row in enumerate (card_levels)] flatten_cards = np.array(unfolded_cards).flatten() result = 0 for i in range (1 , len (flatten_cards)): if flatten_cards[i] < flatten_cards[i-1 ]: result -= 1 return result
空格数
1 2 3 4 class MinMax : def empty (self, card_numbers, card_levels ): return np.sum (card_levels == 0 )
最大指数值
1 2 3 4 class MinMax : def max_level (self, card_numbers, card_levels ): return np.max (card_levels)
重复指数
用字典先统计所有数字出现的次数,然后将所有次数累加。
1 2 3 4 5 6 7 8 9 10 11 12 13 class MinMax : def repeat (self, card_numbers, card_levels ): dic = {} for number in card_levels.flatten(): if number != 0 : dic[number] = dic.get(number, 0 ) result = 0 for value in dic.values(): result += value-1 return -value
平均数
1 2 3 4 class MinMax : def average (self, card_numbers, card_levels ): return np.mean(card_levels)
MinMax类
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 import copyimport numpy as npimport Gameai_max_depth = 6 ai_params = (1.0 , 2.0 , 3.0 , 1.0 , 0 , 0 ) class MinMax : def __init__ (self, gameinstance ): self.game = gameinstance def get_numbers (self ): return self.game.getcards() def get_levels (self ): return np.array([[int (np.log2(n)) if n != 0 else 0 for n in row] for row in self.get_numbers()], dtype=int ) def solve (self, params, depth ): pass def alpha (self, params, max_depth, current_depth=1 , alpha_val=-np.inf, beta_val=np.inf ): pass def beta (self, params, max_depth, current_depth=1 , alpha_val=-np.inf, beta_val=np.inf ): pass def evaluate (self, params ): methods = (self.smooth, self.mono, self.empty, self.max_level, self.repeat, self.average) card_numbers = self.get_numbers() card_levels = self.get_levels() result = 0 for i in range (len (methods)): current_method_value = float (methods[i](card_numbers, card_levels)) result += current_method_value*params[i] return result def smooth (self, card_numbers, card_levels ): pass def mono (self, card_numbers, card_levels ): pass def empty (self, card_numbers, card_levels ): pass def max_level (self, card_numbers, card_levels ): pass def repeat (self, card_numbers, card_levels ): pass def average (self, card_numbers, card_levels ): pass def play (game, params=ai_params, max_depth=ai_max_depth, animate=True ): game.init() ai = MinMax(game) while not game.game_over: ai_res = ai.solve(params, max_depth) game.step(ai_res, animate) game.routine() if ai_res == Game.IDLE: game.game_over = True def main (): game = Game.Game2048(False ) play(game) input ('press any key to exit: ' ) if __name__ == '__main__' : main()
调参实验
虽然我们定义了一些用来组成评估函数的不同维度,可是应该怎么组织它们呢?我决定做一些实验,看每一种参数对于游戏结果的影响。
各参数的影响
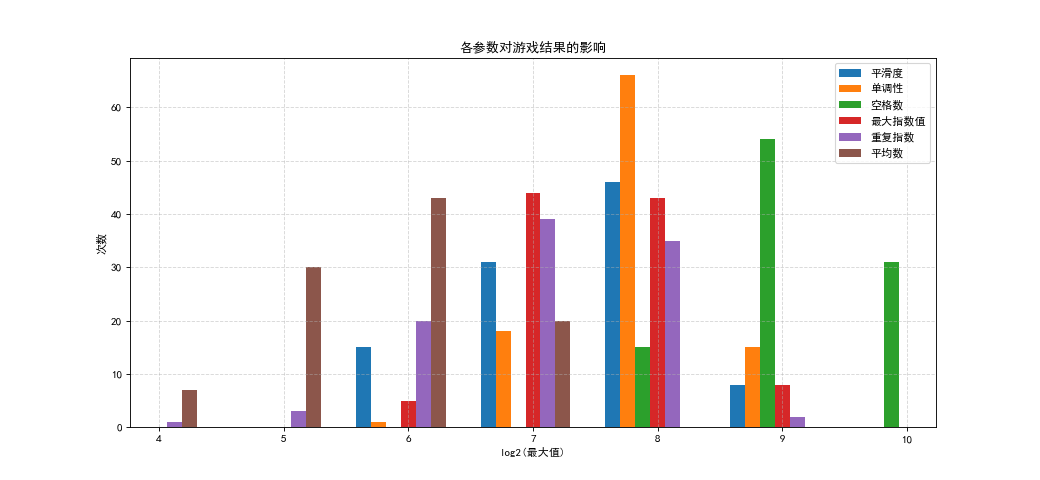
我们分别测试不同的评估函数,每种评估函数只会使用上面提到的六个维度中的一种,搜索深度为6,分别进行100次实验,将每次游戏结束时场面上最大的数字取对数记录下来,画出了下面的图:
怎么看这个图呢?比如很显眼的很高的那个橙色,意思是如果评估函数只考虑单调性,游戏有非常大的概率结束的时候最大的数字是28 =256。
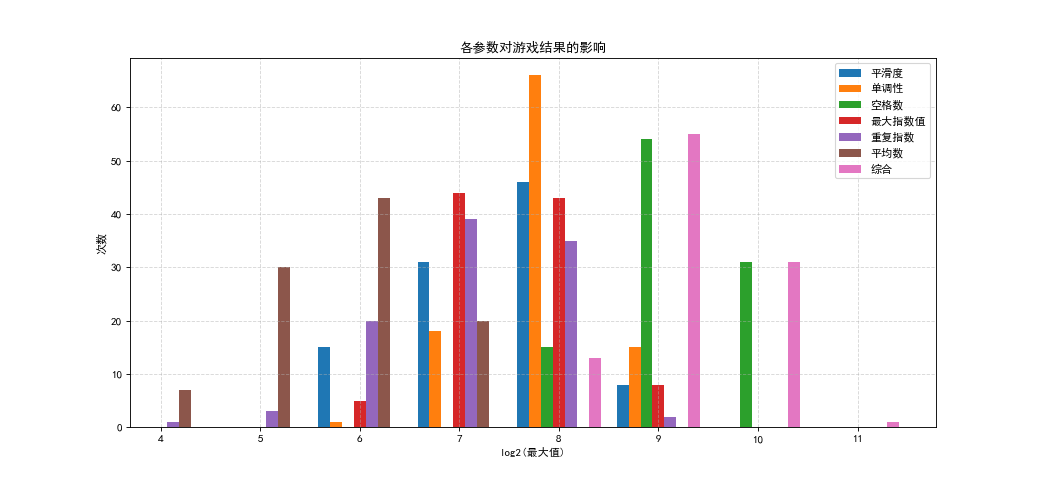
参数综合
有了上面对于各个参数的影响的直观认识,我们设定如下参数:
平滑度 1.0
单调性 2.0
空格数 3.0
最大指数值 1.0
重复指数 0.0
平均数 0.0
当然这个参数还是定得太草率了,如果能对评估函数做更进一步的研究,对参数做更细分的调整,相信游戏表现会比现在好很多。不过经过这么一些学习和实验,现在我已经对Min-Max算法有了比较好的掌握,已经达到目的了。