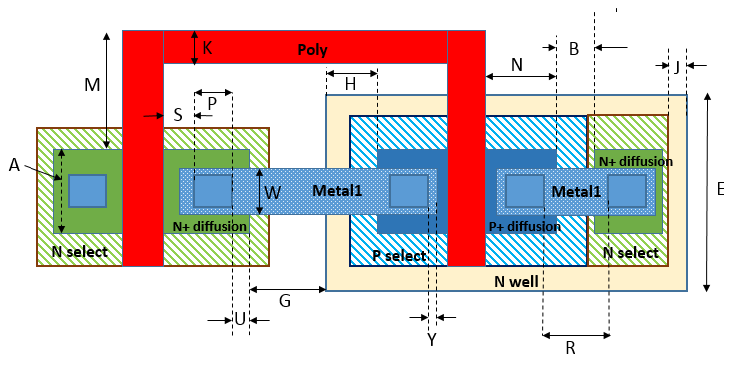
EDA流程学习 - 设计规则检查（DRC）

参考：《Electronic Design Automation for IC Implementation, Circuit Design, and Process Technology》Chapter 20

INTRODUCTION

制造设计：(Design for Manufacturability, DFM)，是一种方法和技术，旨在确保设计能够在制造过程中高效、可靠地生产出来。
模式匹配：(Pattern Matching, PM)，是一种验证设计规则的方法。
多段光刻技术：(Multi-Patterning Technology, MPT)，是一种用于曝光光刻的技术。

CONCEPTS

验证时，几何图形被分组到层中：

Drawn layers 表示原始布局数据，输入验证系统时图形会被合并，消除几何重叠或相邻。
Polygon layers 作为层创建操作（如布尔运算、拓扑多边形操作或几何测量函数）的输出。
Edge layers 表示合并多边形的边缘，按长度、角度或其他属性分类。
Error layers 包含 DRC 空间测量的一个到四个边缘的聚类，用于图形结果表示。

DESIGN FOR MANUFACTURING

使用属性来记录单个对象或多个对象集合的抽象信息，属性是包含数值或字符串值（可能同时包含）的属性，允许对对象进行分类。

基于方程的 DRC 检查允许用户使用关系方程的组合来过滤一个或多个层，并为每个层上的对象分配属性结果。

PATTERN MATCHING

PM 工具有以下主要功能：

允许用户构建模式，包括相对于模式中其他元素的空间固定元素或可移动元素。
存储模式库中的各个模式。
从模式库中选择一部分模式。
搜索设计并选择与模式匹配的区域。
呈现结果。

PM 工具能够找到确切的或者模糊的匹配。

MULTI-PATTERNING

当创建小物体时，一个单独的绘制层被分成两个部分。DRC 的物理验证步骤包括检查一个绘制层是否可以分成两个（或更多）输出掩膜层，并满足一组对象之间重叠和间距的关系约束。这种能力被称为多段光刻技术（MPT）。

掩膜层分割成两个图案：

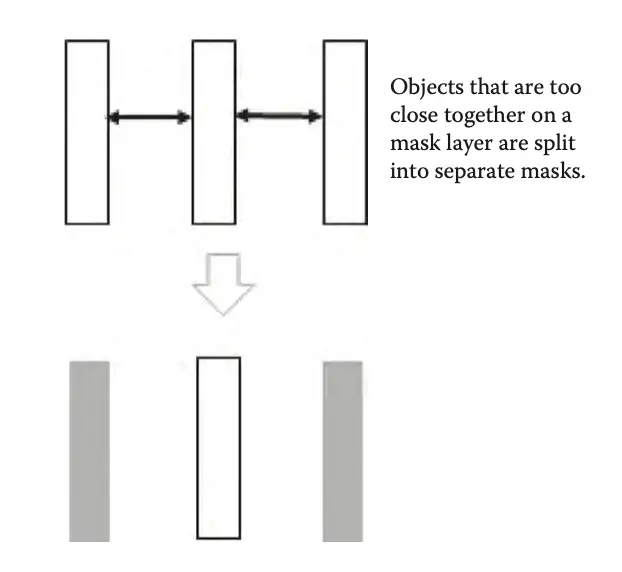
有时候，这些物体无法被分组，这时 DRC 工具就会使用冲突环或冲突路径来报告这种错误：

有一种解决冲突的方法是使用缝合线。

理想情况下，每个分割掩膜的制造过程应该是相同的，这意味着分割层在原掩膜层的范围内应该具有大致相同的密度。

WHEN TO PERFORM DRC

单元创建和快组装的设计阶段
块与布线区域之间的区域以及从块到布线区域的过渡的验证
完整芯片组装完成后，DRC 操作可能还会创建填充物对象，在在宽金属路线中插入槽，创建和分析光刻近邻修正的特征，或者插入半分辨率辅助特征（SRAFs，或散射棒）
SoC 设计要在设计的交互式和批处理阶段进行检查
完整芯片阶段，DRC 用于验证设计是否可以进行制造

FLAT DRC

在进行设计规则检查之前将整个设计展开，将所有的短圆和模块合并为一个大的单元。

优势是简化了设计规则检查的过程；限制是有可能会导致一些误报和漏报。

HIERARCHICAL DRC

利用物理布局设计中的输入设计层次结构和其他重复样式，识别设计中只需分析一次然后重复使用的块，从而显著减少验证时间。

GEOMETRIC ALGORITHMS FOR PHYSICAL VERIFICATION

SCAN LINE-BASED ANALYSIS（扫描线分析）

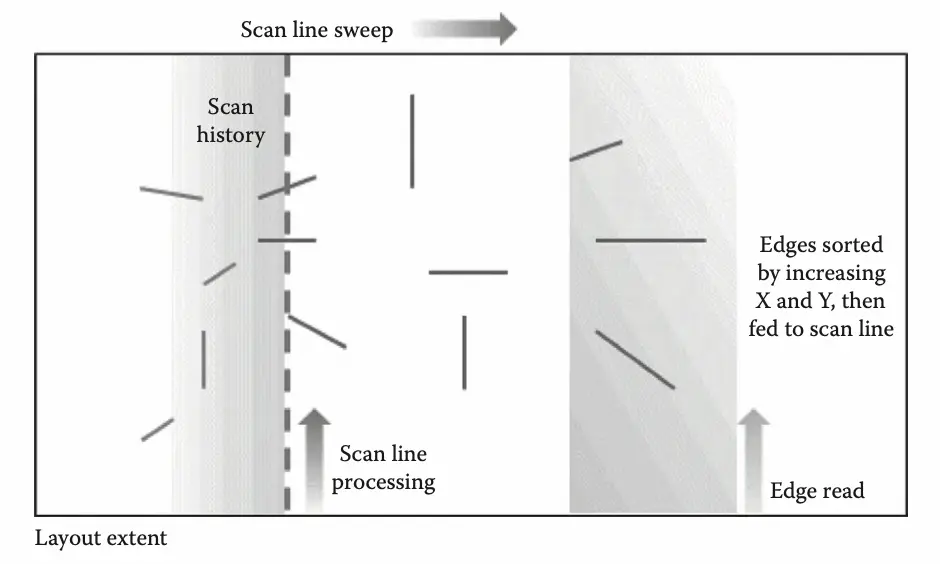
实际情况下，与扫描线相交的对象数量为 $O(\sqrt{n})$ ，故扫描线分析的时间复杂度为 $O(\sqrt{n} × \sqrt{n}) = O(n)$ 。
这是一种乐观的估计，大多数实现在 $O(n \ log \ n)$ 和 $O(\sqrt{n})^3$ 之间。

通常，大多数实现都使用边缘或梯形表示。边缘表示具有直接表示所分析几何体的优势。梯形是通过沿任一轴将输入多边形分割而形成的，提供了一些性能优化，但由于分割造成的虚假边界，需要额外的簿记复杂性。
通过扩展扫描线以具有一定宽度，使用历史带、分离或距离。可以方便地处理关系。
增强扫描线，包括高级几何捕捉舍入算法。

HIERARCHICAL DATA STRUCTURES

层次布局验证包括以下概念：

内在几何（Intrinsic geometries）：给定一层 L 和一个单元 C，在层 L 上，单元 C 的内在几何是在层 L 上的形状（几何），是层 L 上每个 C 的实例所共有的。
交互几何（Interaction geometries）：给定一层 L 和一个单元 C，在层 L 上，单元 C 的交互几何是在层 L 上的内在几何与单元 C 在层次结构的较高位置相交的区域。
提升（Promotion）：根据需要将内在几何向上移动到层次结构中，以获得足够的单元特定上下文以准确执行操作的过程。

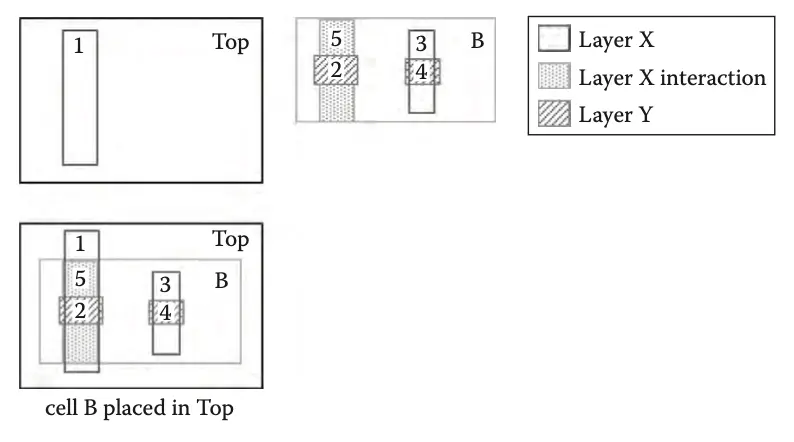
区域交互和提升

考虑如下操作：Z = X Boolean AND Y

如下图，单元格 B 被放置在单元格 Top 中时，对象 1 时单元格 Top 中的内在几何，对象 2、3 和 4 时单元格 B 中的内在几何。对象 5 是一个交互几何，显示了 Top 中对象 1 与单元格 B 中的重叠部分。

首先在单元格 B 中执行与操作。对象 3 和 4 离 5 足够远，在 B 中执行与操作。对象 2 和 5 的交集被提升到单元格 Top 中。由于不需要再进行提升操作，在单元格 Top 中完成与操作。结果如下：

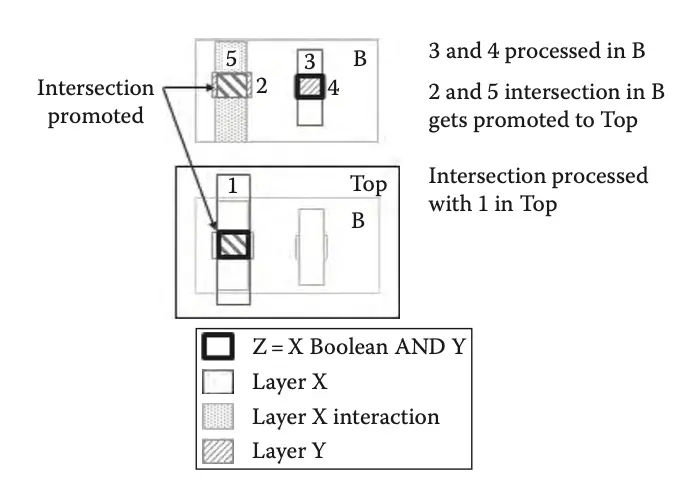
层 Z 包含两个内在几何，一个在单元格 Top 中，一个在单元格 B 中。在单元格 B 中还创建了一个 Z 交互几何，显示了 Top 中内在 Z 形状的重叠部分。，这个交互几何将与对象 2 和 5 的交集重合。

连通性模型

连通性模型将一个层或多个层之间的几何交互封装成与几何关联的逻辑结构。

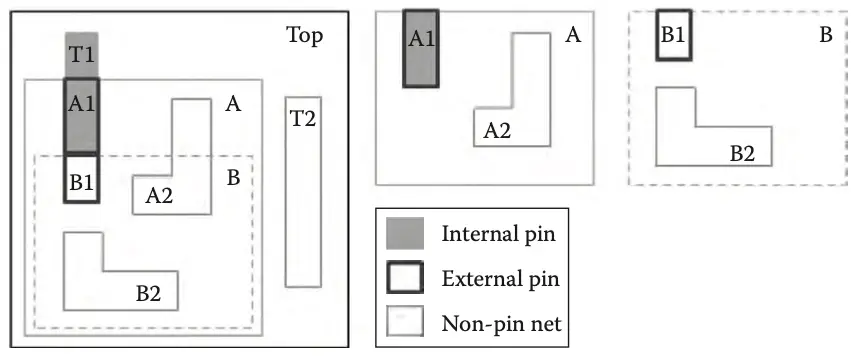
内部引脚与单元的层次子树内的网络连接，外部引脚与单元的层次子树外的网络连接。
例如下图中，网络 B1 时单元 B 的外部引脚。当单元 B 被放置在单元 A 中时，B1 连接到 A1。网络 A1 是单元 A 的外部引脚。当单元 B 被放置在 A 中时，网络 A1 也是单元 A 的内部引脚。当单元 A 被放置在顶层单元中时，网络 A1 连接到网络 T1，即顶层单元的内部引脚。网络在顶层单元中被认为是完整的。网络 B2、A2 和 T2 在父单元外部没有连接，因此它们不是引脚。

多边形连通模型

多边形连通模型确定了在特定层上哪些几何图形相互作用。多边形连通模型对于需要有关多边形的拓扑操作非常有用。

节点连通性

完整的连通性序列包括所有互联层，如下面的伪代码所示：

connect M1 and POLY through CONTACT
connect M1 and M2 through VIA1
connect M2 and M3 through VIA2
...

这种连通性对于基于连通性的 DRC 检查、设备识别和电路拓扑提取至关重要。

有一次性确定和逐层递增地构建完整的电气网络两种方式。

PARALLEL COMPUTING

DRC 工具必须支持 SMP 和分布式架构，以及两者的组合。
两个途径实现并行处理：基于单元的并行处理和基于操作的并行处理。

PROSPECTS

将有更多挑战！