数据结构实验 - 寻找有向无环图（DAG）中的路径

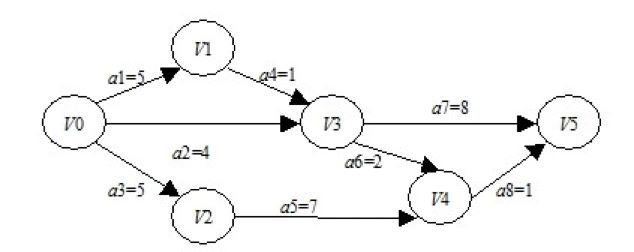
在一个有向无环图（DAG）中，有节点Vertices，连接两个节点的叫做边Edges，每条边都有权重Weight，指定一个起点，一个终点和X个中间点，用C++编写程序，找出经过所有这些指定点的权重之和的前TopN条路径。需要自己设计图的数据结构，构造相应单元测试用例（可以用GoogleTest），用例要覆盖X为1个或者多个，N为1条或者多条，并能运行通过测试用例。

程序设计

题目已经给出足够多的信息，可以依此直接创建Graph类而无需进行需求分析。类图如下：

图的创建与修改

我希望创建一个尽可能动态的图，这个图可以在任意时候新增或者删除节点，也可以在任意时候增加或者去除某条边，或改变某条边的权重。

使用邻接矩阵来表示图，定义了结构Edge用来表示一条边，定义了结构Path用来表示一条寻得的路径。

//
//  graph.hpp
//  DAG
//
//  Created by 郭帆 on 2023/7/21.
//

#ifndef graph_hpp
#define graph_hpp

struct Edge {
    int from = 0;
    int to = 0;
    int weight = 0;
};

struct Path {
    int weight;
    std::vector<int> pathpoint;
};

class Graph {
private:
    int _vertices_count;
    std::vector<std::vector<int>> _edges;
    
public:
    Graph(int size, std::vector<std::vector<int>> edges) : _vertices_count(size), _edges(edges) {}
    Graph(int size = 0) {
        *this = Graph(size, std::vector<std::vector<int>>(size, std::vector<int>(size, 0)));
    }
    
    bool addVertices(int number);
    bool insertVertex(int index);
    bool removeVertex(int index);
    
    bool setEdge(Edge e);
    bool setEdge(std::vector<Edge> v);
    
    bool isDAG();
    std::vector<Path> findPath(int from, int to, std::vector<int> pathpoint);
    
private:
    std::vector<bool> __visited;
    std::vector<int> __next;
    void DFS(int from, int to, std::vector<int> &pathpoint, std::vector<Path> &result);
};

#endif /* graph_hpp */

图有两个构造函数

• 指定图的大小和邻接矩阵
• 指定图的大小，邻接矩阵初始化为0

对于图的顶点来说，有三个方法对它们进行操作：

• addVertices：在末尾添加指定数量的顶点，会扩充邻接矩阵的大小
• insertVertex：在指定位置插入一个顶点，会扩充邻接矩阵的大小
• removeVertex：删除指定位置的顶点，会减小邻接矩阵的大小

bool Graph::addVertices(int number) {
    if (number <= 0) return false;
    
    // resize existing lines
    for (int i = 0; i < _vertices_count; i++) {
        _edges[i].resize(_vertices_count + number);
    }
    
    // add new lines
    for (int i = 0; i < number; i++) {
        _edges.push_back(std::vector<int>(_vertices_count + number, 0));
    }
    
    // refresh vertices amount
    _vertices_count += number;
    
    return true;
}

bool Graph::insertVertex(int index) {
    if (index < 0 || index > _vertices_count) return false;
    
    // insert column
    for (int i = 0; i < _vertices_count; i++) {
        _edges[i].insert(_edges[i].begin() + index, 0);
    }
        
    // insert row
    _edges.insert(_edges.begin() + index, std::vector<int>(_vertices_count + 1, 0));
    
    // refresh vertices count
    _vertices_count++;
    
    return true;
}

bool Graph::removeVertex(int index) {
    if (index < 0 || index >= _vertices_count) return false;
    
    // remove line
    _edges.erase(_edges.begin() + index);
    
    // remove column
    for (int i = 0; i < _vertices_count-1; i++) {
        _edges[i].erase(_edges[i].begin() + index);
    }
    
    // refresh vertices count
    _vertices_count--;
    
    return true;
}

有两个方法操作图的边(setEdge)，删除边即将边的权重设置为0：

• 使用一个Edge结构来修改边
• 使用一个Edge的vector批量设置边

bool Graph::setEdge(Edge e) {
    if (e.from >= _vertices_count || e.from < 0 ||
        e.to >= _vertices_count || e.to < 0) {
        return false;
    }
    _edges[e.from][e.to] = e.weight;
    return true;
}

bool Graph::setEdge(std::vector<Edge> v) {
    bool result = true;
    for (auto &e : v) {
        if (!setEdge(e)) result = false;
    }
    return result;
}

isDAG使用拓扑排序方法判断图中是否有环，即判断图是否为有向无环图。

bool Graph::isDAG() {
    __visited = std::vector<bool>(_vertices_count, false);
    
    int cnt = 0;
    bool finished = false;
    auto edges = _edges;
    while (!finished) {
        bool contain_zero_degree = false;
        for (int i = 0; i < _vertices_count && !__visited[i]; i++) {
            
            // find degree for vetex i
            int degree = 0;
            for (int j = 0; j < _vertices_count; j++) {
                if (edges[j][i] > 0) degree++;
            }
            
            // degree is 0
            if (!degree) {
                contain_zero_degree = true;
                cnt++;
                __visited[i] = true;
                
                // clear degree for vetices from vertex i
                for (int j = 0; j < _vertices_count; j++) {
                    edges[i][j] = 0;
                }
            }
        }
        finished = !contain_zero_degree;
    }
    
    return cnt == _vertices_count;
}

寻找路径

为了寻找符合要求的路径，最简单的思路是寻得所有路径，并做筛选：

1. 使用DFS遍历图中不走回头路的所有路径
2. 使用一个__next数组用来回溯路径节点
3. 使用一个__visited数组用来标记已经访问过的节点

std::vector<Path> Graph::findPath(int from, int to, std::vector<int> pathpoint) {
    std::vector<Path> result;
    
    __visited = std::vector<bool>(_vertices_count, false);
    __next = std::vector<int>(_vertices_count, 0);
    
    DFS(from, to, pathpoint, result);
    
    return result;
}

void Graph::DFS(int from, int to, std::vector<int> &pathpoint, std::vector<Path> &result) {
    __visited[from] = true;
    if (from == to) { // path found
        Path p = {};
        int k = 0;
        
        // record pathpoint
        while(k != to) {
            p.pathpoint.push_back(k);
            k = __next[k];
        }
        p.pathpoint.push_back(k);
        
        // calculate path weight
        for (int i = 0; i < p.pathpoint.size() - 1; i++) {
            p.weight += _edges[p.pathpoint[i]][p.pathpoint[i+1]];
        }
        
        // search if middle point in path
        bool is_match = true;
        for (auto m : pathpoint) {
            if (std::find(p.pathpoint.begin(), p.pathpoint.end(), m) == p.pathpoint.end()) {
                is_match = false;
            }
        }
        
        // valid path, push to result
        if (is_match) {
            result.push_back(p);
        }
        
        return;
    }

    // DFS
    for (int j = 0; j < _vertices_count; j++) {
        if(__visited[j] == false && _edges[from][j] != 0) {
            __next[from] = j;
            DFS(j, to, pathpoint, result);
            __visited[j] = false;
        }
    }
}

实验

编写如下代码用来测试Graph类是否满足要求：

//
//  main.cpp
//  DAG
//
//  Created by 郭帆 on 2023/7/21.
//

#include <iostream>
#include "graph.hpp"

using namespace std;

void show_path(vector<Path> path) {
    cout << path.size() << " paths in total. " << endl;
    for (auto p : path) {
        for (auto v : p.pathpoint) {
            cout << v << "->";
        }
        cout << " w: " << p.weight << endl;
    }
    cout << endl;
}

int main(int argc, const char * argv[]) {
    Graph g(5);
    
    g.setEdge({
        {0, 1, 5},
        {0, 3, 4},
        {0, 2, 5},
        {1, 3, 1},
        {2, 4, 7},
        {3, 4, 2}
    });
    
    g.addVertices(1);
    
    g.setEdge({3, 5, 7});
    g.setEdge({4, 5, 1});
    
    auto path = g.findPath(0, 5, {3});
    show_path(path);
    
    path = g.findPath(0, 5, {});
    show_path(path);
    
    path = g.findPath(0, 5, {1, 4});
    show_path(path);
    
    cout << "DAG? " << g.isDAG() << endl;
    g.setEdge({4, 0, 3});
    cout << "DAG? " << g.isDAG() << endl;
    
    return 0;
}

得到输出如下：

4 paths in total. 
0->1->3->4->5-> w: 9
0->1->3->5-> w: 13
0->3->4->5-> w: 7
0->3->5-> w: 11

5 paths in total. 
0->1->3->4->5-> w: 9
0->1->3->5-> w: 13
0->2->4->5-> w: 13
0->3->4->5-> w: 7
0->3->5-> w: 11

1 paths in total. 
0->1->3->4->5-> w: 9

DAG? 1
DAG? 0

可以知道程序各部分运行正常。

按权重排序

对于“找出经过所有这些指定点的权重之和的前TopN条路径”，即“top k”问题，常用堆数据结构来解决，对应C++中即为priority_queue。

修改findPath方法，使其返回一个优先队列：
std::priority_queue<Path> findPath(int from, int to, std::vector<int> pathpoint);

修改DFS方法中的实现，将路径保存到一个优先队列中。

修改Path结构，让其能够使用优先队列，具体来说是重载其<运算符：

struct Path {
    int weight;
    std::vector<int> pathpoint;
    
    friend bool operator<(Path p1, Path p2) { return p1.weight < p2.weight; }
};

修改显示函数，使用优先队列的遍历方式：

void show_path(priority_queue<Path> path) {
    cout << path.size() << " paths in total. " << endl;
    while (!path.empty()) {
        Path p = path.top();
        for (auto v : p.pathpoint) {
            cout << v << "->";
        }
        cout << " w: " << p.weight << endl;
        path.pop();
    }
    cout << endl;
}

再次运行程序，得到输出：

4 paths in total. 
0->1->3->5-> w: 13
0->3->5-> w: 11
0->1->3->4->5-> w: 9
0->3->4->5-> w: 7

5 paths in total. 
0->1->3->5-> w: 13
0->2->4->5-> w: 13
0->3->5-> w: 11
0->1->3->4->5-> w: 9
0->3->4->5-> w: 7

1 paths in total. 
0->1->3->4->5-> w: 9

DAG? 1
DAG? 0

可以看出路径已经被正确排序，问题得到解决。

使用 hash

注意到匹配路径是否符合要求的过程需要两层循环，时间复杂度比较高，所以考虑使用 hash，将原本O(n^2)的时间复杂度降低到O(n)。

元素筛选，第一反应想到效率非常高的 bloom filter，最初的设想是将中间路径点设置为 bloom filter，然后匹配一遍寻得的所有路径，由于 bloom filter 的特性，所需要的路径一定在经过初级筛选之后的子集中，接着对子集做精确的匹配，就能找到筛选结果。
而遍历路径时建立 hash map，再遍历中间节点，同时查询 hash map，时间复杂度也是O(n)。若图的顶点数目非常多，寻得的路径数量可能非常多时，可以研究一下是否使用 bloom filter 会减少程序运行时间。

这里我们先不采用 bloom filter 的方式，留作以后与学长老师们讨论。

void Graph::DFS(int from, int to, std::vector<int> &pathpoint, std::priority_queue<Path> &result) {
    __visited[from] = true;
    if (from == to) { // path found
        // ...
        
        // search if middle point in path
        std::unordered_set<int> s;
        for (auto point : p.pathpoint) {
            s.emplace(point);
        }
        bool is_match = true;
        for (auto m : pathpoint) {
            if (s.find(m) == s.end()) {
                is_match = false;
            }
        }

        // ...
    }

    // ...
}

Cmake

文件目录结构为：

.
├── CMakeLists.txt
├── include
│   └── graph.hpp
├── main.cpp
└── src
    └── graph.cpp

CMakeLists.txt内容为：

# 声明要求的cmake最低版本
cmake_minimum_required(VERSION 3.15)

# 声明一个cmake工程
project(assignment1)

# 打印相关消息
MESSAGE(STATUS "my first cmake project")

# 设置路径
set(EXECUTABLE_OUTPUT_PATH ${PROJECT_SOURCE_DIR}/build)

# 设置头文件路径
include_directories(${PROJECT_SOURCE_DIR}/include)

# 编译静态库
add_library(graph STATIC ${PROJECT_SOURCE_DIR}/src/graph.cpp)

# 编译可执行文件
add_executable(${PROJECT_NAME} main.cpp)

# 链接需要的库
target_link_libraries(${PROJECT_NAME} graph)

# gtest
target_link_libraries(${PROJECT_NAME} libgtest.a libgtest_main.a pthread)

# compile_commands.json中包含所有编译单元执行的指令
set(CMAKE_EXPORT_COMPILE_COMMANDS ON)

# 打包功能
set(CPACK_PROJECT_NAME ${PROJECT_NAME})
set(CPACK_PROJECT_VERSION ${PROJECT_VERSION})
include(CPack)

Google test

加入 GTest 的测试代码：

TEST(testCase, test0) {
    Graph g(6);
    
    g.setEdge({
        {0, 1, 5},
        {0, 3, 4},
        {0, 2, 5},
        {1, 3, 1},
        {2, 4, 7},
        {3, 4, 2},
        {3, 5, 7},
        {4, 5, 1}
    });
    
    EXPECT_EQ(g.findPath(0, 5, {3}).size(), 4);
}

int main(int argc, char ** argv) {
    // google test
    testing::InitGoogleTest(&argc, argv);
    
    return RUN_ALL_TESTS();
}

执行如下指令：

mkdir build
cd build
cmake ..
make
./assignment1

运行结果如下：

[==========] Running 1 test from 1 test suite.
[----------] Global test environment set-up.
[----------] 1 test from testCase
[ RUN      ] testCase.test0
[       OK ] testCase.test0 (0 ms)
[----------] 1 test from testCase (0 ms total)

[----------] Global test environment tear-down
[==========] 1 test from 1 test suite ran. (0 ms total)
[  PASSED  ] 1 test.