《计算几何——算法与应用（第三版）》学习笔记1 - 扫描线（第1-4章）

系列文章
-> 《计算几何——算法与应用（第三版）》学习笔记1 - 扫描线（第1-4章）
《计算几何——算法与应用（第三版）》学习笔记2 - 空间索引（第5-7章）
番外篇
计算几何 - C++ 库的调研
 Boost C++ Libraries学习 - Geometry
Boost C++ Libraries学习 - Boost.Polygon (GTL)

计算几何：导言

Voronoi 图（Voronoi diagram），可以为覆盖多个城市的商业区域建立模型，指挥机器人，甚至描述和模拟晶体的生长过程。

凸包的例子

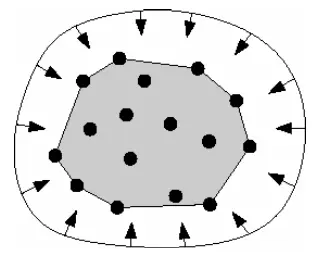
平面的一个子集 $S$ 被称为是“凸”的，当且仅当对于任意两点 $p, q ∈ S$ ，线段 $\overline{pq}$ 都完全属于 $S$ 。
集合 $S$ 的凸包 $CH(S)$ ，就是包含 $S$ 的最小凸集——更准确地说，它是所有包含 $S$ 的所有凸集的交集。
可以将平面有限点集 $P$ 的凸包定义为：顶点取自于 $P$ 且包含 $P$ 中所有点的那个唯一的凸多边形（convex polygon）。

所以计算出一个点集的凸包可以取所有点对，如果其他所有点都在这两个点组成的直线一侧（如右侧），则说明这两个点在凸包上。这种方法的时间复杂度是 $O(n^3)$

有一些特殊情况：

点有可能在线上，这就是所谓的“退化情况”（degenerate case）。
浮点运算（floating point arithmetric）带来的舍入误差（rounding error）可能导致找出多余的边，或少找一些边。

有一个更好的递增式算法（incremental algorithm）：

对点集按照 $x$ 轴排序。
按照顺序每次将一个点加入集合中。
若集合中最后三个点构成一个左拐（left-turn），则删除最后三个点中居中的点；如果集合中的点数大于三，就再做检查，直到集合中最后三个点构成的是右拐（right-turn）。
上面是上凸包（upper hull）的构造过程，下凸包（lower hull）的构造思路是相似的。

有两种特殊情况：

存在 $x$ 坐标相同的点，那么排序时需在 $x$ 坐标相同时比较 $y$ 坐标。
判断左拐还是右拐时，有可能三个点共线，这时也需要删除居中的点。

【定理 1.1】
给定包含 $n$ 个点的任意一个平面点集，其凸包都可以在 $O(nlogn)$ 时间内构造出来。

退化及鲁棒性

先考虑一般情况，做一些假设，忽略特殊情况。之后再将特殊情况集成进算法中。
实现过程中会出现鲁棒性（robustness）的问题，一种方法是借助于某个支持精确运算（exact arithmetic）的软件包，另一种方法是调整算法，使之能够检测到可能出现的不一致问题，并采取适当的措施以避免程序崩溃。

应用领域

计算机图形学
机器人学
地理信息系统（GIS）
CAD/CAM
其他应用领域
- 分子建模
- 模式识别（pattern recognition）

线段求交：专题图叠合

为了增加地图的可读性，地理信息系统将（不同类型的）信息划分为若干层（layer）。每一层都是一副专题图（thematic map）。

线段求交

线段求交问题（line segment intersection problem）

定义交点需要确定线段是否为闭的，如果是闭的，那么一条线段的端点落在另一条线段上，则相交。

如果依次检查每一对线段，看它们是否相交，这种算法需要 $O(n^2)$ 的时间。但大多数情况下焦点数会远小于平方量级。所以需要一种运行时间不仅取决于输入中线段的数目，还取决于（实际的）交点数目。这样的算法被称为“输出敏感的”算法（output-sensitive algorithm）。在这个问题上可以称为“交点敏感的”（intersection-sensitive）。

引入平面扫描线算法（plane sweep algorithm）。

扫描线（sweep line）：虚拟的线，通过移动扫描线会与几何做交互。
状态（status）：随着扫描线的推进，扫描线会遇到某些事件点，此时扫描线的状态需要更新。
事件点（event point）：就本算法而言，是各线段的端点。
状态结构（status structure）：保存了某个时刻与扫描线相交的线段。例如扫描线遇到的事件点是线段的上端点，则需要将线段插入到状态结构中，若是下端点则需删去。

当引入一条线段到状态结构中时，需要将其与自身的上端点左、右紧邻的线段进行交点测试。此后，当扫描线推进到某个新的位置时，与某条线段紧邻的邻居有可能发生变化，此时，需要将它与新的邻居进行测试。所以状态结构不仅要在端点处进行更新，也需要在交点处更新。

引理 2.1
设两条非水平的线段 $s_i$ 和 $s_j$ 只相交于其内部的一点 $p$ ，而且，任何第三条线段都不经过 $p$ 。则在（扫描线到达）高于 $p$ 的某个事件点处（时）， $s_i$ 和 $s_j$ 必然会彼此紧邻，并因此接受相交测试（于是对应的交点将被发现）。

定理 2.4
给定由平面上任意 $n$ 条线段构成的一个集合 $S$ 。可以在 $O(nlogn+Ilogn)$ 时间内，使用 $O(n)$ 空间，报告出 $S$ 中各线段之间的所有交点，以及与每个交点相关的所有线段。其中， $I$ 为实际的交点总数。

双向链接边表

（doubly-connected edge list）

一种用来表示由图的平面嵌入（planar embeddings of graph）而导出的平面子区域划分问题的数据结构。只要原来的图是连通的，其对应的子区域划分就必然也是连通的。原图中每个节点（node）的嵌入，称为一个顶点（vertex）；原图中每条弧（arc）的嵌入，称为一条边（edge）。子区域划分的“面”（face）指的是在平面上除去所有的顶点和所有的边之后，余下的每一个极大的连通子集。

本章中讨论的边是开的，面也是开的（其边界由子区域划分的某些边和点围成）。所谓一个子区域划分的复杂度，就是构成该子区域划分的顶点、边和面的总数。

若一个顶点是某条边的端点，就说这个顶点与这条边是关联的（incident）。一张面与其边界上的每条边、每个顶点也是关联的。

这个数据结构要能完成以下操作：

围绕指定的某张面，沿其边界遍历（traverse）一周；
在指定一条公共边之后，通过与其相邻于一侧的面，找到另一侧的那张面；
在给定一个顶点之后，（依次）枚举出与之关联的所有边。

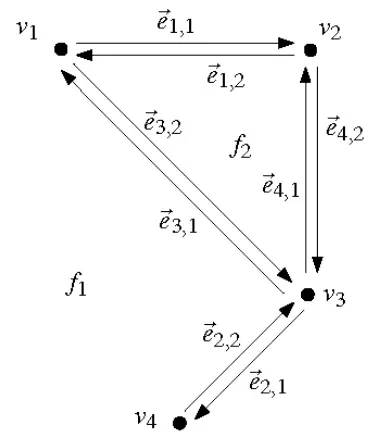
双向链接边表中会存储附加信息或者说属性信息（attribute information），用来扩展图的含义。这种数据结构中，一条边被当作两条边用，像劈竹子一样劈开，得到的叫做半边（half edge），两条半边方向相反，互为孪生兄弟（twin），但其左侧都是与它所关联的面。半边的起点（origin）与终点（destination）互相颠倒重合。

双向链接边表由三组记录构成：一组对应于顶点，一组对应于面，还有一组对应于边。举例以及三张表的结构如下：

Vertex	Coordinates	IncidentEdge
$v_1$	$(0,4)$	$\vec{e}_{1,1}$
$v_2$	$(2,4)$	$\vec{e}_{4,2}$
$v_3$	$(2,2)$	$\vec{e}_{2,1}$
$v_4$	$(1,1)$	$\vec{e}_{2,2}$

Face	OuterComponent	InnerComponents
$f_1$	$nil$	$\vec{e}_{1,1}$
$f_2$	$\vec{e}_{4,1}$	$nil$

Half-edge	Origin	Twin	IncidentFace	Next	Prev
$\vec{e}_{1,1}$	$v_1$	$\vec{e}_{1,2}$	$f_1$	$\vec{e}_{4,2}$	$\vec{e}_{3,1}$
$\vec{e}_{1,2}$	$v_2$	$\vec{e}_{1,1}$	$f_2$	$\vec{e}_{3,2}$	$\vec{e}_{4,1}$
$\vec{e}_{2,1}$	$v_3$	$\vec{e}_{2,2}$	$f_1$	$\vec{e}_{2,2}$	$\vec{e}_{4,2}$
$\vec{e}_{2,2}$	$v_4$	$\vec{e}_{2,1}$	$f_1$	$\vec{e}_{3,1}$	$\vec{e}_{2,1}$
$\vec{e}_{3,1}$	$v_3$	$\vec{e}_{3,2}$	$f_1$	$\vec{e}_{1,1}$	$\vec{e}_{2,2}$
$\vec{e}_{3,2}$	$v_1$	$\vec{e}_{3,1}$	$f_2$	$\vec{e}_{4,1}$	$\vec{e}_{1,2}$
$\vec{e}_{4,1}$	$v_3$	$\vec{e}_{4,2}$	$f_2$	$\vec{e}_{1,2}$	$\vec{e}_{3,2}$
$\vec{e}_{4,2}$	$v_2$	$\vec{e}_{4,1}$	$f_1$	$\vec{e}_{2,1}$	$\vec{e}_{1,1}$

在实际的问题中，需要定制化地增删记录内容。有些实现中，可能会要求子区域划分的顶点和边所对应的图必须是连通的，为此，需要引入一些虚边（dummy edge）。

计算子区域划分的叠合

给定两个子区域划分 $S_1$ 和 $S_2$ ，其叠合记作 $O(S_1, S_2)$ 。

叠合算法首先将 $S_1$ 和 $S_2$ 所对应的两个双向链接边表复制到一个新的双向链接边表中，通过计算两个边网络之间的交点，并适当地将两个双向链接边表中的相关部分链接起来，最终把这个新的双向链接边表转化为对应于 $O(S_1, S_2)$ 的一个合法的双向链接边表。
使用扫描线算法，在遇到一个事件点时，如果涉及到的边分别来自不同的子区域划分，则对新的双向链接边表做局部调整，保证扫描线扫过的区域已经被调整好。由于调整操作的复杂度不会超过线段求交算法的复杂度，所以可以在 $O(nlogn + klogn)$ 时间内计算出 $O(S_1, S_2)$ 所对应双向链接边表中所有顶点记录和半边记录，其中 $n$ 为 $S_1$ 和 $S_2$ 的总体复杂度，而 $k$ 为二者叠合结果的复杂度。
对于面，需要更复杂的操作。大致思路是构造一个图 $G$ ，图的每一个节点对应一个环。利用这个图的节点，可以为每一连通子块生成一张面。而标记这张面属于原先的哪个子区域划分，则是看其顶点位于原子区域划分的哪个面内。

判断一个环是面的边界还是空洞的边界的方法是：找到环中最左端的顶点 $v$ （若有多个则选最低者），看与之相关联的两条边朝这张面内部所张的角度，小于 $180°$ 则是外边界；否则就是空洞的边界。

TODO: 面的设置

定理 2.6
给定任意两个平面子区域划分 $S_1$ 和 $S_2$ ，其复杂度分别为 $n_1$ 和 $n_2$ ，令 $n = n_1 + n_2$ 。则可以在 $O(nlogn + klogn)$ 时间内计算出 $S_1$ 和 $S_2$ 的叠合，其中 $k$ 为叠合结果的复杂度。

布尔运算

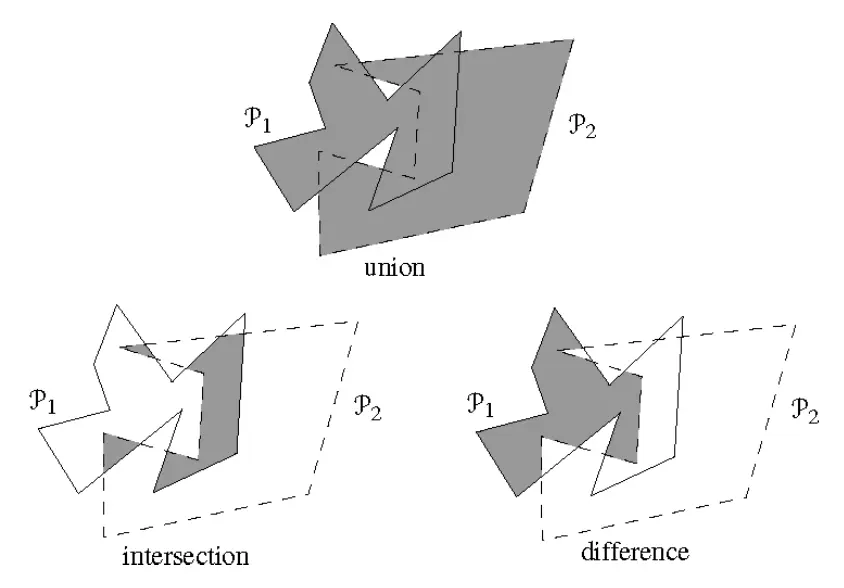
地图叠合算法是一个强有力的工具，在众多不同的应用中它都可以大显身手。其中特别有用的一点，就是可以用以实现两个多边形 $P_1$ 和 $P_2$ 的布尔运算（boolean operation）——并（union）、交（intersection）和差（difference）。

推论 2.7
任意给定两个多边形 $P_1$ 和 $P_2$ ，设其顶点数分别为 $n_1$ 、 $n_2$ ，令 $n := n_1 + n_2$ 。则可以在 $O(nlogn + klogn)$ 时间内，计算出 $P_1 ∩ P_2$ 、 $P_1 ∪ P_2$ 或 $P_1 \backslash P_2$ ，其中 $k$ 为最终输出的复杂度。

多边形三角剖分：画廊看守

艺术画廊问题（art gallery problem）

看守与三角形剖分

对于多边形内部的任何一个点，只要联接于它与某台摄像机之间的开线段完全落在多边形的内部，它就能被这台摄像机监视到。“计算出特定多边形所需摄像机的最小数目”这一问题，是 NP-hard 问题。

通过极大的一组互不相交的对角线（diagonal），可将一个多边形分解为多个三角形——称作该多边形的三角剖分（trangulation）。
三角形剖分的例子：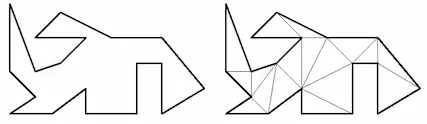

定理 3.1
任何简单多边形都存在（至少）一个三角形剖分；若其顶点数目为 $n$ ，则它的每个三角形剖分都恰好包含 $n - 2$ 个三角形。

由于顶点可能与多个三角形关联，所以把摄像机安排在顶点上。使用“对经过三角形剖分后的多边形的 3-染色（3-coloring）”来对多边形顶点进行染色。每个三角形三个顶点的颜色各异，相同颜色不会出现在一个三角形的一条边上。选用数量最少的那个颜色的点用来安排摄像机，则所需要的摄像机数目不会超过 $⌊{n \over 3}⌋$ 。

一种获得 3-染色方案的办法是构建它的“对偶图”，其中，每个三角形作为图的顶点，若两个三角形共用一条对角线，则在图里面设置一条弧。由于对角线会把原多边形一分为二，所以对偶图是一棵树。从树的任意顶点开始遍历这棵树，第一个节点染上三种不同颜色，往后每到一个新顶点，由于这个顶点和上一个顶点有公共的边，而公共的边已经被染色完成，所以只需染一种颜色。

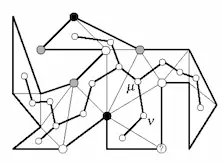
至此已经给出了艺术画廊问题的一个上届（upper bound）。

定理 3.2
包含 $n$ 个顶点的任何简单多边形，只需（放置在适当位置的） $⌊{n \over 3}⌋$ 台摄像机就能保证：其中任何一点都可见于至少一台摄像机。有的时候，的确需要这样多台摄像机。

定理 3.3
任给一个包含 $n$ 个顶点的简单多边形 $P$ 。总可以在 $O(nlogn)$ 时间内，在 $P$ 中确定 $⌊{n \over 3}⌋$ 台摄像机的位置，使得 $P$ 中的任何一点都可见于其中的至少一台摄像机。

多边形的单调块划分

利用定理 3.1 的证明方式进行三角形剖分需要平方级的时间复杂度。而对凸多边形（convex polygon）的三角形剖分可以在线性时间内完成，可是将多边形划分为多个凸块的难度与对它做三角形剖分是一样的。因此我们将思路转变为把多边形划分为“单调块”（monotone piece）。

如果对任何一条垂直于 $l$ 的直线 $l'$ ， $l'$ 与该多边形的交都是连通的，则称作简单多边形“关于某条直线 $l$ 单调”（monotone with respect to a line $l$ ）。连通的意思就是 $l'$ 与多边形的交或者是一条线段，或者是一个点，也可能是一个空集。
更直观的理解是垂直于 $l$ 的直线 $l'$ ，只会把多边形分割为两个或者一个，不会更多。
如果一个多边形关于 $y$ 坐标轴单调，则称它是 $y$ -单调的（ $y$ -monotone），这个多边形被称作 $y$ -单调多边形（ $y$ monotone polygon）。它的一个特征是在沿着多边形的左（右）边界，从最高顶点走向最低顶点的过程中，我们是周都是朝下方（或者水平）运动，而绝不会向上。

把多边形的顶点分为五类，其中有四种拐点：起始顶点、分裂顶点、终止顶点以及汇合顶点。另一种是普通顶点。

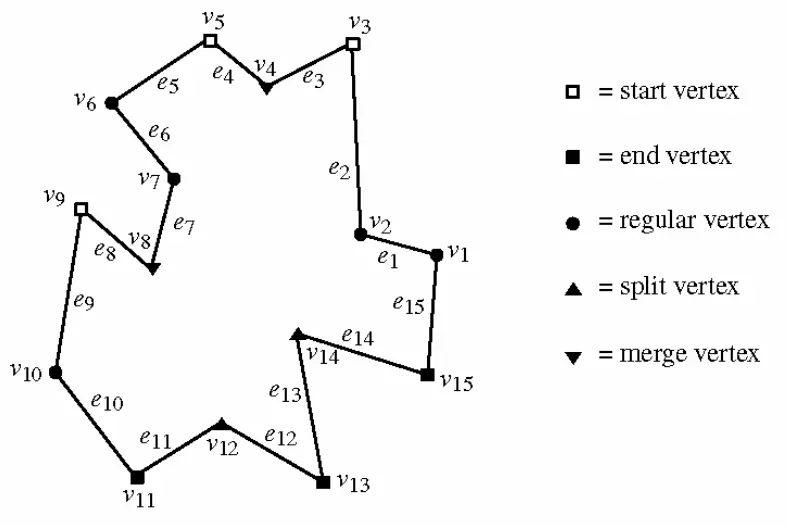
起始顶点（start vertex）：与它相邻的两个顶点的高度都比它低，而且在该点处的内角小于 $\pi$ ；
分裂顶点（split vertex）：与它相邻的两个顶点的高度都比它低，而且在该点处的内角大于 $\pi$ ；
终止顶点（end vertex）：与它相邻的两个顶点的高度都比它高，而且在该点处的内角小于 $\pi$ ；
汇合顶点（merge vertex）：与它相邻的两个顶点的高度都比它高，而且在该点处的内角大于 $\pi$ ；
普通顶点（regular vertex）：除上述顶点外的所有顶点。

有了这些定义，就可以利用平面扫描算法来对多边形进行单调块划分。

引理 3.4
一个多边形若既不包含分裂顶点，也不含汇合顶点，则必然是 $y$ -单调的。

如上图，先将顶点与边的对应关系确定好，顶点逆时针排列为 $v_1,v_2,...,v_n$ ，边 $e_i=\overline{v_i v_{i+1}},1 \le i \lt n$ ；另外， $e_n = \overline{v_n v_1}$ 。
使用一条扫面线从上往下扫描，所有顶点被放到优先队列中，优先级的设置是顶点坐标 $y\uparrow$ ，其次是坐标 $x\downarrow$ 。（因为过程中不会产生新的事件点，所以使用其他排序算法先做排序也是可以的）
需要引入一个“助手”的概念：当扫描线遇到某个分裂顶点 $v_i$ 时，从扫描线的状态结构中可以得到与 $v_i$ 相邻的左、右两条边，令它们分别为 $e_j$ 、 $e_k$ ，那么介于两条边之间的那些位于 $v_i$ 上方的顶点中，找到最低的那个，称作“ $e_j$ 的助手（helper of $e_j$ ）”，记作 helper( $e_j$ )。正式的定义是“在位于扫描线上方、通过一条完全落在 $P$ 内部的水平线段与 $e_j$ 相联的那些顶点中，高度最低的那个顶点”。
那么消除分裂顶点的办法就是分别将它们与各自左侧那条相邻边的助手相联。
而对于汇合顶点 $v_i$ ，扫描线到达它时，它就会成为它左侧那条边 $e_j$ 的助手，当 $e_j$ 的助手需要被替换时，判断其旧助手是否为汇合顶点，如果是，就在新、老助手之间引入一条对角线。若 $e_j$ 的助手一直是 $v_i$ ，直到扫描完成也没有改变，则将这个助手与 $e_j$ 的下端点联接起来。

定理 3.6
使用 $O(n)$ 的存储空间，可以在 $O(nlogn)$ 时间内将包含 $n$ 个顶点的任何简单多边形分解为多个 $y$ -单调的子块。

单调多边形的三角剖分

使用贪婪算法（greedy algorithm），在线性时间内，完成对单调多边形的三角剖分。
思路是从上往下遍历顶点，使用一个栈用来存储那些已经遍历过，但任可以产生更多对角线的顶点。
当遍历到一个顶点 $u_j$ 时，判断其是在栈顶顶点的同一侧还是对面的一侧。对于对面侧的顶点，将其与栈内（除栈低元素）外的每一个顶点联对角线，并将 $u_j$ 和 $u_{j-1}$ 压入栈中；对于同一侧的顶点，依次检查它与栈顶元素的联线是否完全落在 $P$ 的内部，若是则联线，弹出栈顶，最后将不能联线的两个顶点压入栈中。

定理 3.7
由 $n$ 个顶点组成的任一严格 $y$ -单调多边形，都可以在线性时间内被三角剖分。

定理 3.8
使用 $O(n)$ 的存储空间，可以在 $O(nlogn)$ 时间内对由 $n$ 个顶点组成的任一简单多边形进行三角剖分。

定理 3.9
使用 $O(n)$ 存储空间，可以在 $O(nlogn)$ 时间内对包含 $n$ 个顶点的任一平面子区域划分进行三角剖分。

线性规划：铸模制造

铸造中的几何

引理 4.1
沿着某个方向 $\vec{d}$ 通过一次平移，多面体 $P$ 能够从其铸模中提取出来，当且仅当相对于 $P$ 的每一张普通面的外法失， $\vec{d}$ 与之所成的角度都至少为 90°。

普通面（ordinary facet）：多面体除了顶面之外的其他任一面。
外法失（outward normal）：铸模上某个面与空洞方向相反方向的法线。

引理 4.1 说明的是当三维多面体从铸模中移出时，普通面要么是沿着铸膜运动，要么是远离它。当 $\vec{d}$ 与普通面的外法失角度小于 90° 时，意味着这一面有朝着铸模内部运动的趋势，必然会被铸模挡住。

根据【引理 4.1】可以得出一个推论：若可以通过多次小幅度的平移将 $P$ 抽取出来，则必然可以仅通过一次平移就将它抽取出来。

考虑平面 $z=1$ ，其上的每一个点 $(x,y,1)$ 对应一个从原点出发的方向 $(x,y,1)$ ，这个方向是相对于铸模顶面 $z=0$ 的朝上的方向，这些方向才是有可能将多面体从铸模中取出的方向，而平面 $z=1$ 也包含了所有这些朝上的方向。
那么对于一个外法失 $\vec{η}=(\vec{η_x}, \vec{η_y}, \vec{η_z})$ ，方向 $\vec{d}=(d_x, d_y, 1)$ 与其所成的夹角不小于 90° 可以使用它们的点积为正来限制：

\vec{η_x}d_x + \vec{η_y}d_y + \vec{η_z} ≤ 0

多面体的每一个非水平普通面，会在平面 $z=1$ 上留下一条线，而上述不等式确定了在平面 $z=1$ 上这根线应取哪一边（闭集）的区域。这样的话若最后这些区域交集非空，则其中的任何一个点，都对应于一个可以将 $P$ 顺利抽取出来的方向。反之说明不可能将 $P$ 从铸模中抽取出来。

定理 4.2
任给由 $n$ 张小平面围成的多面体 $P$ 。使用 $O(n)$ 空间，可在 $O(n^2)$ 时间内判断 $P$ 是否可铸造的。果真如此，还可在同样长的时间内，计算出一个可行的铸模，以及将 $P$ 从中抽取出来的具体方向。

半平面求交

一个双线性约束条件（linear constraint） $a_i x + b_i y ≤ c_i$ 确定了 $R^2$ 空间中的一张闭的半平面，其边界为直线 $a_i x + b_i y = c_i$ 。下图是半平面相交的几种可能情况。

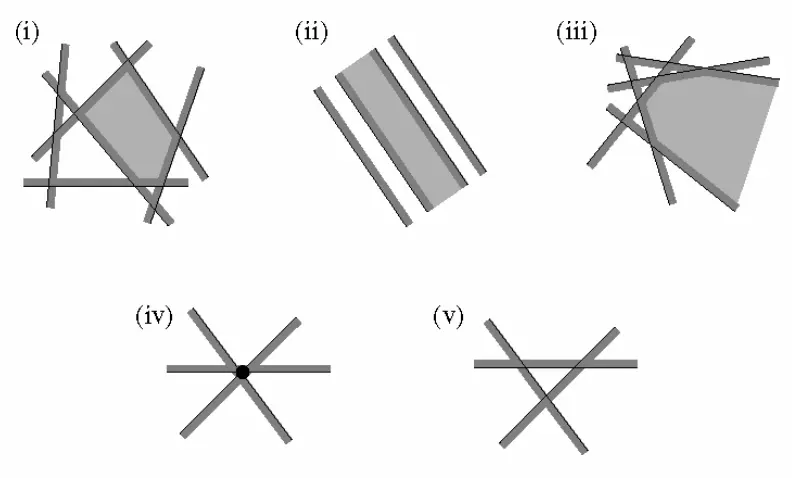
一种方法是，使用分治法，利用【专题图叠合】章节的条件 可以在 $O(nlogn+klogn)$ 时间内，计算出任意两个多边形的交 这一结论。当只有一个半平面时，只需返回这一半平面，否则就将半平面数量一分为二，分别求其多边形交，再对两个结果求多边形交。这种做法的时间复杂度为 $O(nlog^2n)$ 。

但注意到这种半平面交集的形状为凸多边形（convex polygon），利用这一性质可以有更高效的算法。
对于两个凸多边形求交，使用扫描线算法时可以确定同一时间扫描线上最多有 4 条线（每两条分别来自两个多边形区域的左、右边界），而下一个事件点也是在这 4 条线的下端点中最高的那一个。

定理 4.3
平面上任意两个凸多边形区域的交集，都可以在 $O(n)$ 时间内计算出来。

推论 4.4
给定平面上的一组共 $n$ 张半平面，可以使用线性的空间，在 $O(nlogn)$ 时间内计算出其公共的交集。

递增式线性规划

与排序算法一样，任何可以对一组半平面求交的算法，在最坏情况下必须话费 $\Omega(nlogn)$ 时间。

但铸造问题只需要求得一个可行解即可，这与运筹学（operations research）中的线性优化（linear optimization）问题，或者称作线性规划（Linear Programming）问题密切相关。
运筹学中有许多线性规划算法，如著名的单纯形法（simplex algorithm）。但这题中要求解的是低维线性规划（low-dimensional linear programming），使用计算几何中发展起来的方法。

上图展示了一个线性规划 $(H, \vec{c})$ 解的四种情况：

待解的线性规划问题是不可行的，亦即，对应的约束条件集是空的。
沿着方向 $\vec{c}$ ，可行解域是无界的。此时存在某条射线 $ρ$ 完全落在可行解域 $C$ 中——沿该射线，函数 $f_{\vec{c}}$ 的取值可以任意增长。果真如此，我们就要求算法描述出这样的一条射线。
可行解域的边界上有一条边 $e$ ，其外法失的方与 $\vec{c}$ 相同。在这种情况下，虽然该线性规划问题时有解的，却不唯一——实际上，在 $e$ 上的任一点处，函数 $f_{\vec{c}}(p)$ 都达到了最大。
只要不是前面的那三种情况，就肯定有解，而且解是唯一的——这个解是 $C$ 的某个顶点，而且这个顶点时沿着方向 $\vec{c}$ 的极点。

引入两个附加的约束条件：

m_1 := \begin{cases} p_x≤M & c_x>0 \\ -p_x≤M & otherwise \end{cases}

m_2 := \begin{cases} p_y≤M & c_y>0 \\ -p_y≤M & otherwise \end{cases}

加入这两个约束条件是为了将可能出现的无界区域变成有界区域，保证每次维护的只有一个最优解，而不是一条射线。同时，为了排除解与可行解域的某条边重合的情况，约定同时有多个解时，按照字典序取最小的解。这样原问题就转化成了一个有界线性规划问题（bounded linear program），此时每个线性规划问题都是可行的，解也是唯一的，而且这个解必然时可行解域的某个顶点，这个顶点称作最优解顶点（optimal vertex）。

有了以上前提，就可以进行递增式线性规划了。遍历所有半平面，当遍历到 $h_i \in H_i$ 时，若旧的最优解顶点 $v_{i-1} \in h_i$ ，则 $v_i = v_{i-1}$ ；否则要么 $C_i = \varnothing$ ，要么 $v_i \in l_i$ （其中 $l_i$ 是 $h_i$ 的边界）。
当引入的半平面不包含旧的最优解顶点 $v_{i-1}$ 时，由以上结论，我们只需要从 $h_i$ 的边界去寻找新的最优解顶点 $v_i$ 。思路是考察 $x$ 坐标，将这一个小的问题退为一维线性规划问题。

这一算法使用的是线性的空间，时间复杂度为 $O(n_2)$ 。

随机线性规划

上一节讲的算法，其性能与遍历半平面的顺序相关，所以需要一种找到好的遍历顺序的方法，但这件事也是难事。

所以使用随机次序（random ordering），因为大多数的次序都会导致一个快速的计算过程。为了分析随机算法的性能，我们使用算法的期望运行时间（expected running time）来衡量——也就是全部共 $n!$ 种可能排列次序的平均运行时间（average running time）。

引理 4.8
任一包含 $n$ 个约束条件的二维线性规划问题，都可以在 $O(n)$ 的期望运行时间内得到解答；而且，所需要的空间在最坏情况下也不会超过线性规模。

期望的线性律（linearity of expectation）：一组随机变量总和的期望值，等于这些随机变量各自期望值的总和。

无界线性规划问题

前面为了避免无界线性规划，引入了两个附加约束条件，但实际问题中还是存在无界线性规划问题的，研究无界线性规划问题的解法是有必要的。

引理 4.9
一个线性规划问题是无界的，当且仅当存在某个矢量 $\vec{d}$ 满足 $\vec{d} \cdot \vec{c} > 0$ 的，同时使得对于任何 $h \in H$ ，不仅有 $\vec{d} \cdot \vec{η}(h) ≥ 0$ ，而且若令 $H' = \{h \in H: \vec{η}(h) \cdot \vec{d} = 0\}$ ，则线性规划问题 $(H', \vec{c})$ 总是可行的。

$\vec{d}$ ：解的射线的方向。
$\vec{c}$ ：函数 $f\vec{c}$ 的方向。
$H$ ：半平面集合。
$\vec{η}(h)$ ：半平面指向可行解域一侧的法失。

于是我们可以找出一个一维线性规划问题来判定一个二维线性规划问题是否无界。思路如下：

旋转坐标系，使得 $\vec{c}$ 朝下，即 $\vec{c} = (0, 1)$ 。
将 $\vec{d}$ 规范化为 $\vec{d} = (d_x, 1)$ 。
给定一个单位矢量 $\vec{η}(h) = (η_x, η_y)$ ，则 $\vec{d} \cdot \vec{η}(h) ≥ 0$ 就可以转化成不等式： $d_x η_x ≥ -η_y$ 。
将所有上述不等式当作一个一维线性规划问题 $\overline{H}$ 的 $n$ 个约束条件。
$H'$ 有解的情况下，由于有一个子集 $H' ⊆ H$ ，使得 $\overline{H}$ 的一个可行解 $d_x^*$ 对于 $H'$ 中的每一个半平面都有 $d_x^* η_x + η_y = 0$ ，而且它们的外法失都与 $d$ 垂直，意味着 $H'$ 中所有边界线相互平行，用 $x$ -坐标轴对它们求交之后，将再次得到一个一维线性规划问题，用来确认 $H'$ 是不是可行的。
$H'$ 没有一个可行解的情况下， $(H, \vec{c})$ 必然有界（看引理）。

定理 4.10
即使在最坏情况下，使用不超过线性规模的空间，也可以在 $O(n)$ 的随机期望运行时间内，对包含 $n$ 个约束条件的任何二维线性规划问题进行求解。

$^*$ 高维空间中的线性规划

定理 4.12
对于每一固定的维数 $d$ ，任何含有 $n$ 个约束条件的 $d$ -维线性规划问题，都可以在 $O(n)$ 的期望运行时间内得到解答。

但是随着维度的升高， $n$ 的系数将急速增长，所以只有在维数不高的情况下，该算法才是有用的。

$^*$ 最小包围圆

给定由平面上 $n$ 个点所组成的一个集合 $P$ ，试找出 $P$ 的最小包围圆（smallest enclosing disc）——亦即，包含 $P$ 中所有点、半径最小的那个圆。使用一个随机增量式算法（randomized incremental algorithm）来解决这个问题。将 $P$ 中的点打乱，然后遍历它，动态地维护最小包围圆。
前面的线性规划问题由一个条件：每加入一张半平面，只要此前的最优解顶点包含于其中，就不必对其进行修改；否则，新的最优解顶点必然位于这个新版空间的边界上。对于现在这个问题，也有类似的性质。每次引入一个点，判断其是否在上一次求出的最小包围圆内部，若是则不需要更新最小包围圆。

引理 4.14
设 $P$ 为平面上的一个点集；设 $R$ 为另一个（允许为空的）点集，而且 $P ∩ R = \varnothing$ ；设点 $p \in P$ 。则有下列命题成立：

如果存在某个圆覆盖了 $P$ ，而且其边界穿过 $R$ 中的所有点，那么这样的圆中必然存在唯一的最小者，记作 $md(P, R)$ 。

如果 $p \in md(P \backslash \{p\}, R)$ ，那么 $md(P, R) = md(P \backslash \{p\}, R)$ 。

如果 $p \notin md(P \backslash \{p\}, R)$ ，那么 $md(P, R) = md(P \backslash \{p\}, R ∪ \{p\})$ 。

定理 4.15
平面上任意一组共 $n$ 个点的最小包围圆，可以在 $O(n)$ 的期望运行时间内计算出来，而且为此需要的空间在最坏情况下不会超过线性规模。