《计算几何——算法与应用(第三版)》学习笔记2 - 空间索引(第5-7章)
系列文章
《计算几何——算法与应用(第三版)》学习笔记1 - 扫描线(第1-4章)
-> 《计算几何——算法与应用(第三版)》学习笔记2 - 空间索引(第5-7章)
番外篇
计算几何 - C++ 库的调研
Boost C++ Libraries学习 - Geometry
Boost C++ Libraries学习 - Boost.Polygon (GTL)
正交区域查找:数据库查询
将数据库中的每条记录对应到多维空间中的一个点,这样就可以将本来针对记录的查询变成针对点的查询。例如下图,把“yyyymmdd”格式的日期作为 x 坐标,把“月收入”作为 z 坐标,把“家庭成员数量”作为 y 坐标,图中的立方体就可以作为“查询出生于 1950 年至 1955 年之间、月收入在 $3000 至 $4000 之间并且家庭成员有 2 到 4 人的所有员工”的几何化表示。
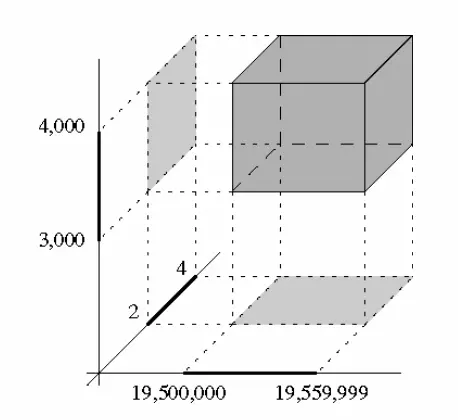
有了这种表示,接下来要解决的问题是如何找到落在这个立方体中的点。在计算几何中,这类查询被称为矩形区域查询(rectangular range query),或者正交区域查找(orthogonal range query)。
一维区域查找
对于一维的区域查找问题(range searching problem),使用平衡二分查找树来解决。
对区域的左边和右边数值分别做一次查找,这两次查找结果之间的所有叶子结点则是区域查找的结果。
一个优化手段是只有某个节点将查询区域分隔开,才需要对两棵子树分别搜索。
由于查询时间跟需要输出的点的数量有关,所以算法是输出敏感的(output-sensitive)。
| 空间复杂度 | 构造时间复杂度 | 查询时间复杂度 |
|---|---|---|
定理 5.2
给定由一维空间中任意 n 个点构成的集合 P。可以使用空间,在时间内构造一棵平衡二分查找树以存储 P。这样,可以在时间内查找出任何区间内的所有点(其中,k 是实际被查找出来的点数)。
kd-树
(k-dimensional tree)
每次二维矩形区域查找,都可以分解为两次一维子查找——其中一次沿 x 方向进行,另一次沿 y 方向进行。
将二分查找树的思路扩充到二维,对于深度为偶数的节点,使用垂线进行划分;对于深度为奇数的节点,使用水平线进行划分。每次划分分别存储到当前节点的左、右孩子节点中。2d-树(2维 kd-树,2-dimensional kd-tree)举例如下:
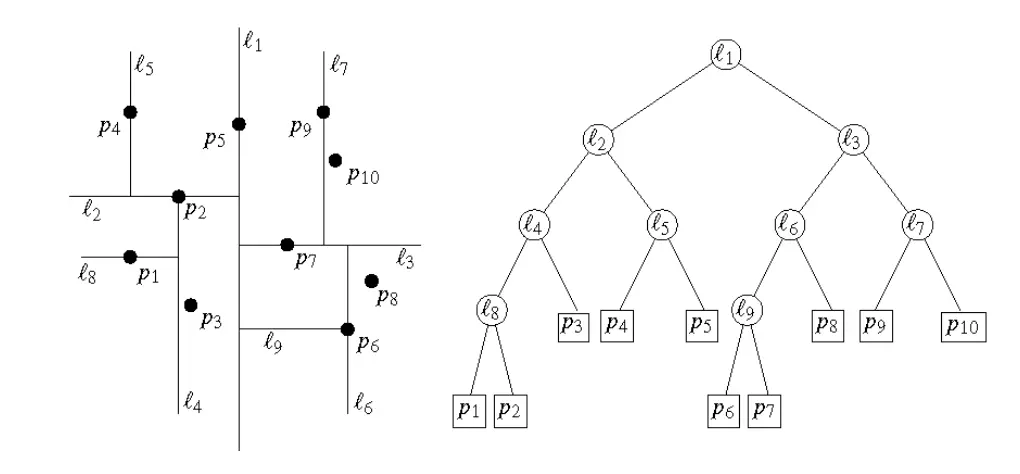
| 空间复杂度 | 构造时间复杂度 | 查询时间复杂度 |
|---|---|---|
引理 5.3
给定由任意 n 个点组成的一个集合,其对应的 kd-树占用空间,并可以在时间内构造出来。
引理 5.4
如果待查询区域为与坐标轴平行的区域,那么对于存储了任意 n 个点的一棵 kd-树,每次查询都可以在时间内完成,其中 k 为实际被报告出来的点数。
定理 5.5
给定由平面上任意 n 个点构成的集合 P,其对应的 kd-树将占用空间,并且可以在时间内构造出来。使用这棵 kd-树,每次矩形区域查找锁需的时间将不会超过,其中 k 为实际被报告出来的点数。
如果要扩展到更高的维度,只需按照维度顺序分割点集即可。
| 空间复杂度 | 构造时间复杂度 | 查询时间复杂度 |
|---|---|---|
区域树
(range tree)
| 空间复杂度 | 构造时间复杂度 | 查询时间复杂度 |
|---|---|---|
其核心思想是用空间换时间,除了建立一棵主树(main tree)之外,还建立一系列小一些的树。主树的每个内部节点或者叶子节点,都存储有一个指针,指向一棵平衡二分查找树,我们称这颗小的二分查找树为节点的联合结构(associated structure)。
- 主树:将 P 中各点按照 x 坐标组织成平衡二分查找树。
- 联合结构:主树中,获得该节点对应的子树,将子树的叶子节点对应的 P 的子集 P’ 再组织成按照 y 坐标为依据的二分查找树。
这种情况下,查询特定矩形区域的点,只需要使用一次一维二分查找,找出 x 坐标落在该矩形区域的 P 的子集,这个子集会对应一系列的联合结构,对这些联合结构再做一维的二分查找,就可以筛选出查询结果。
拥有联合结构的数据结构称为多层次数据结构(multi-level data structure)。主树被称为第一层的树(first-level tree),每一联合结构都被称为第二层的树(second-level tree)。
引理 5.6
给定由平面上任意 n 个点构成的点集,其对应的区域树占用的存储空间。
引理 5.7
若采用区域树来存储(平面上的)任意 n 个点,则与坐标方向平行的每一次矩形区域查询,只需要时间。这里的 k 为实际报出来的点数。
定理 5.8
给定由平面上任意 n 个点构成的集合 P。对应于 P 的一棵区域树占用的存储空间,并且可以在时间内构造出来。对这棵区域树进行查找,可以在时间内,从 P 中报告出落在任一矩形待查区域之内的所有点,其中 k 为实际被报告出来的点数。
如果使用分散层叠(fractional cascading)技术,查询时间还可以进一步改进至。
高维区域树
要创建一棵 d 维的区域树,假设其中点的坐标为,只需按维度一级一级创建联合结构即可。
具体来说就是,将所有点按照组织成一棵平衡二分查找树,对于其中每个节点,我们取出它对应的子树的叶子节点的那个子集,继续按照组织成一棵平衡二分查找树,以此类推,直到使用上最后一维的坐标。
查找时,也是逐级进行搜索,首先使用第一层的树搜索出落在搜索范围内的点点子集,然后使用第二维的树搜索符合要求的点。直到搜索完一维的树,就筛选出所有 d 个维度均落在搜索区域中的点。
定理 5.9
给定由 d 维空间中任意 n 个点构成的集合 P,d≥2。对应于 P 的一棵区域树占用的存储空间,并且可以在时间内构造出来。对这棵区域树进行查找,可以在时间内,从 P 中报告出落在给定(超)矩形待查区域之内的所有点,其中 k 为实际被报告出来的点数。
一般性点集
满足来自某个全序域(totally ordered universe)的点集,可以对其中任意两个坐标进行比较,并可以计算中值。
方法是将原县表示为实数的坐标,替换为来自所谓合成数空间(composite number space)的元素。通俗来说,就是比较时考虑全部维度的数据,如果第一维相同,就比较第二维,以此类推,直到分出大小(例如return p1.x == p2.x ? p1.y > p2.y : p1.x > p2.x;)。按照字典序(lexicographical order),我们可以在合成数空间中定义一个全序(total order)。
由以上方法,前文所述的区域查找就可以支持点的某些坐标相同的情况了。
分散层叠
TODO:思路
定理 5.11
在 d(≥2) 维空间中,给定由任意 n 个点构成的集合 P。总可以在时间内,构造出一棵与 P 对应的层次化区域树,其占用的存储空间为。借助这棵区域树,可以在时间内,报告出 P 中落在某矩形待查区域之内的所有点,其中 k 为实际被报告出来的点数。
注释及评论
空间索引发展历程:
- 首先提出的是四叉树(quadtree),但其在最坏情况下性能相当差。
- 1975 年 Bentley 提出了 kd-树,对四叉树进行改进。
- 之后提出了区域树。
- 再之后提出了分散层叠技术。
- Chazelle 提出了修改后的层次化区域树,是解决二维区域查找问题最有效的数据结构,空间复杂度为。
- 如果查找区域某侧无界,则使用优先查找树(priority search tree),空间复杂度是线性的,时间复杂度为。
- ……
点定位:找到自己的位置
点定位查询(point location query):给定一张地图以及由坐标指定的一个查询点 q,在图中找到 q 所处的子区域。
点定位及梯形图
对于原始的字区域划分,在每个顶点处引入一条垂线,利用这些垂线可以将平面划分为若干垂直的条带(slab)。条带按照 x 坐标有序,所以只需 的时间就可以得到待查询点所处的条带。条带内的直线按照 y 坐标有序,所以也只需 的时间就可以知道待查询点所处的区域。
如果存下每个条带的坐标,以及每个条带中的所有线段,则空间复杂度为 。
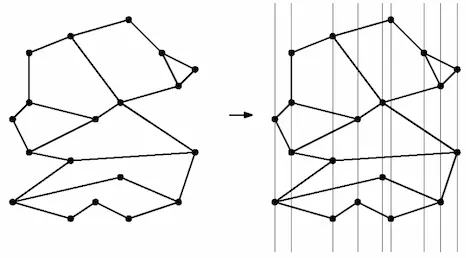
条带可以视作一个子区域划分,即原子区域划分的细分(reginement),条带中的每一张面,都是梯形(trapezoid)、三角形或者类似于梯形的无界面。
若平面上两条线段的交为空,或者只相交于它们的一个共同端点,我们都称它们是互不相交的(non-crossing)。对于平面的任何一个子区域划分,所有边都互不相交。
我们先研究一般性位置线段集(a set of line segments in general position):由 n 条线段构成的集合 S,其中的线段互不相交,都包含在一个包围框(bounding box)R 中,而且任何两个端点都不处于同一条垂线上。
经过 S 中每条线段的左、右端点,向上方和下方各发出一条垂直射线;在碰到 S 中的另一条线段或 R 的边界后,射线终止,这样得到的叫做 S 的梯形图 ,也称作 S 的垂直分解(vertical decomposition)或者梯形分解(trapezoidal decomposition)。由 p 发出的这两条垂直延长线,分别称为 p 的上垂直延长线(upper vertical extension)和下垂直延长线(lower vertical extension)。
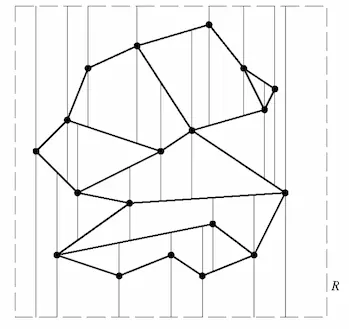
引理 6.1
任意给定一个一般性位置线段集 S,在 S 的梯形图中,每张面都有一到两条垂直的侧边,同时有且仅有两条非垂直的侧边。
引理 6.2
由任意 n 条处于一般性位置的线段组成的集合 S,其梯形图 至多含有 6n+4 个顶点,至多含有 3n+1 个梯形。
如果两个梯形 和 接合于某条垂直边左右,我们就称它们是相邻的(adjacent)。由于做了一般性假设,所以梯形最多只有四个梯形相邻,分别为左上方邻居(upper left neighbour)、左下方邻居(lower left neighbour)、右上方邻居(upper right neighbour)和右下方邻居(lower right neighbour)。
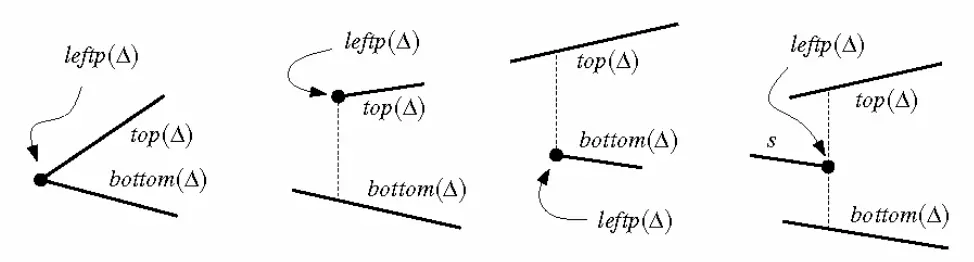
对于每个梯形,无需存储其顶点坐标,而是以 、、 和 来表示,其定义分别如下:
随机增量式算法
(randomized incremental algorithm),用于构造梯形图 和用于点定位的数据结构 。
叫做查找结构(search structure),是一幅有向无环图(directed acyclic graph - DAG)。其中有唯一的根节点,梯形唯一对应于叶子节点。每个内部节点的出度是 2。所有内部节点分为两类:x-节点和 y-节点。每个 x-节点都被标记为 S 中某条线段的一个端点;而每个 y-节点都被标记为某条线段。
查询点 q 位置时,从根节点出发,每个节点都要判断 q 在其两侧的哪一侧(对于 x-节点来说判断左右,对于 y-节点来说判断上下),直到找到某个叶子节点,即点 q 所处的梯形。
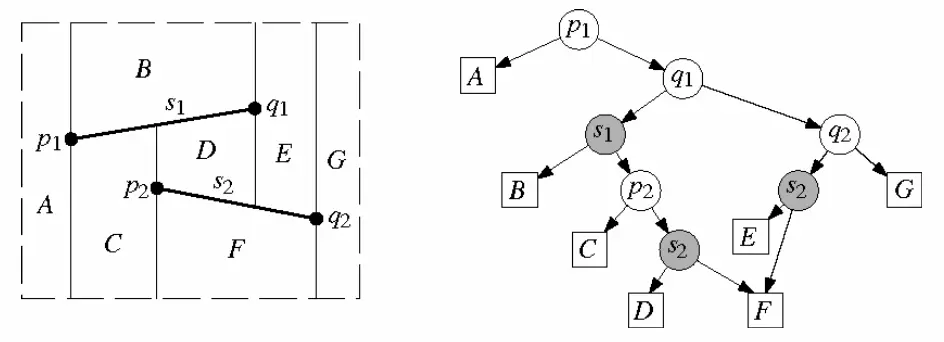
示例中白色圆形为 x-节点,灰色圆形为 y-节点,白色方块为叶子节点。
算法的步骤如下:
- 将子区域划分的线段打乱,以包围盒 R 为最初的梯形图 , 以包围盒 R 作为 的根节点,也是叶子节点。
- 遍历所有线段 ,对当前的 查询线段左端点 所处的梯形 。
- 如果 落在梯形图中已有的端点上,则有两种情况:
- 如果落在某条垂线上,则需将该点往右稍做移动,即选中该垂线右边的梯形;
- 如果落在某条线段上,则需比较两线段的斜率以确定选择上下哪个梯形。
- 利用此梯形寻找其右邻居(右上、右下)中与线段相交的梯形。
- 若 在线段上方,则选中右上邻居,反之亦然。
- 更新 和 。
- 将找到的梯形从 中删除,替换成被 切割后的若干梯形。
- 将 中对应于 的那匹叶子替换成一棵切割后的小树。
- 如果线段跨过了多个梯形,还需考虑梯形的合并。
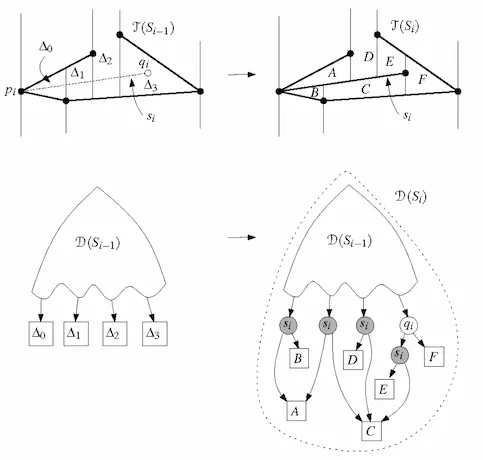
算法的期望性能(expected performance):
定理 6.3
对于由处于一般性位置的任意 n 条线段构成的集合 S,可以在 的期望时间(expected time)内,计算出 S 的梯形图 以及与之对应的查找结构 。该查找结构的期望规模(expected size)为 ;对任何待查询点 q,期望查询时间(expected query time)为 。
这里所指的期望值,仅仅是针对算法能够做出的各种随机选择而言的平均值,而不是对所有可能输入进行平均。因此,不存在坏的输入——也就是说,对由 n 条线段组成的任何输入,该算法的期望运行时间都是 。
最大期望查询时间(expected maximum query time)也是 。
推论 6.4
给定由任意 n 条边构成的一个平面子区域划分 S。可在 期望时间内,构造出一个期望规模为 的数据结构;借助该结构,对任一待查询点的点定位查找,都可以在 期望时间内完成。
退化情况处理
消除前文“一般性假设”的手段。
符号变换(symbolic transformation)用于消除“不同端点不会落在同一条垂线上”的假设。
思路是将坐标系进行一个小角度的旋转,但可能会有计算精度问题。所以使用“剪切变换”(shear transformation)的的仿射变换方法,是一种符号扰动(symbolic perturbation)方法。
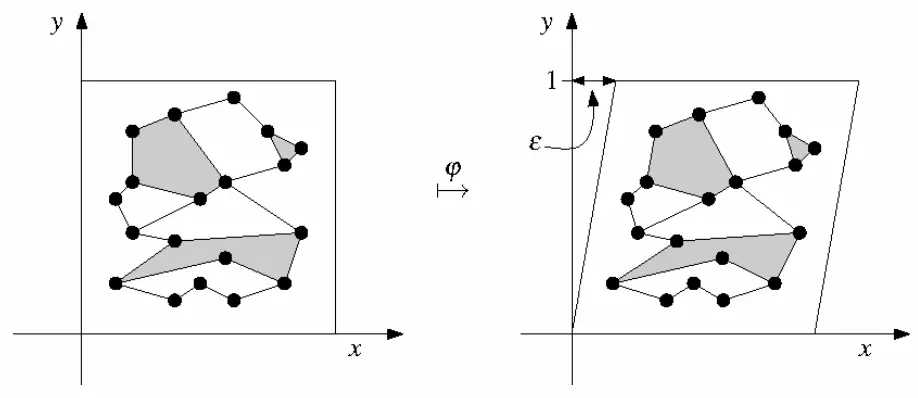
经过这种变换,所有垂线都将成为斜率为 的直线。只要找到足够小的 ,能使得经过剪切变换之后,各输入点在 x 方向的次序不变算法就能正常工作。
定理 6.5
对于由任意 n 条线段构成的集合 S,可以在 的期望时间(expected time)内,计算出 S 的梯形图 以及与之对应的查找结构 。该查找结构的期望规模(expected size)为 ;对任何待查询点 q,期望查询时间(expected query time)为 。
尾分析
虽然最大查询时间可能很长,但这种情况概率很低。高概率上界(high-probability bound)。
引理 6.6
任意给定由 n 条互不相交的线段组成的一个集合 S,一个待查询点 q,以及一个参数 。则在 上对 q 进行查找时,其查找路径上的节点数目超过 的概率,不会超过 。
引理 6.7
任意给定由 n 条互不相交的线段组成的一个集合 S,以及一个参数 。则在 中,查找路径的最大长度超过 的概率,不会超过 。
定理 6.8
任意给定由 n 条边组成的一个平面子区域划分。必然存在支持对 S 进行点定位查询的一个数据结构,它只占用 的存储空间,而且在最坏情况下查找时间不超过 。
注释及评论
点定位有很多方法:
- Edelsbrunner 等人基于线段树(segment tree)和分散层叠(factional cascading)等技术提出的链方法(chain method);
- Kirkpatrick 提出的三角形细分法(triangle reginement method);
- Sarnak 和 Tarjan 以及 Cole 基于持续性(persistency)的方法;
- Mulmuley 提出的随机增量式算法。
动态点定位问题(dynamic point location)中,允许通过增加或删除边,对子区域划分本身进行(动态的)修改。
TODO: 高于二维的点定位问题。