实验3 二叉查找树、红黑树的基本操作实现

实验要求：

  1. 实现下列关于二叉查找树、红黑树的判断、构建、删除等操作。并写出这些操作的流程图或伪代码。
  2. 请说明二叉查找树和红黑树的区别以及时间、空间性能。

Pro1：Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

  1. The left subtree of a node contains only nodes with keys less than the node’s key.
  2. The right subtree of a node contains only nodes with keys greater than the node’s key.
  3. Both the left and right subtrees must also be binary search trees.

对应力扣题：98. 验证二叉搜索树

基本思路

由于BST的前两条性质，所以当遍历到某一个节点时，我们可以知道这个节点的值应该处在的范围。
例如“节点的左子树只包含小于当前节点的数”，那么我们遍历节点的左子树时，可以把当前节点的值传过去，如果左子树出现了大于该值的节点，则说明不符合BST的规则。同理遍历右子树时也可以将当前节点的值作为最小值传下去。
而根节点没有要求，所以访问根节点时我们传来的最大值和最小值分别为LONG_MAX和LONG_MIN。

题解

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool isBetween(TreeNode* node, long long alpha, long long beta) {
        if (!node) return true;
        if (node->val <= alpha || node->val >= beta) return false;
        return isBetween(node->left, alpha, node->val) && isBetween(node->right, node->val, beta);
    }

    bool isValidBST(TreeNode* root) {
        return isBetween(root, LONG_MIN, LONG_MAX);
    }
};

算法复杂度分析

时间复杂度：O(n)，因为需要访问每一个节点，并且每一个节点只遍历一遍。
空间复杂度：O(n)，空间复杂度取决于递归的深度，即树高。而二叉查找树最坏情况下为一条链，树高为n。

Pro2：Red black tree

Construct a red black tree by {1, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}, show the result. Then delet the points in order {14,9,5}, show the result too.

红黑树概念

  1. 每个节点或者是黑色，或者是红色。
  2. 根节点是黑色。
  3. 每个叶子节点是黑色（为空的结点）。
  4. 不能出现两个连续的红色结点（如果一个节点是红色的，那么它的两个子节点都是黑色的）。
  5. 从一个节点开始所有路径上包含相同数目的黑节点。

这篇文章以B树的视角来解释红黑树，非常直观！
TODO

红黑树实现

RBTree.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
#pragma once

#include <iostream>

enum class RBColor { RED = 0, BLACK };

template <typename T>
struct RBTNode {
    enum class RBColor color;
    T key;
    RBTNode* left;
    RBTNode* right;
    RBTNode* p;
};

template <typename T>
class RBTree {
public:
    RBTree() {
        Nil = NewNode();
        root = Nil;
        Nil->color = RBColor::BLACK;
    }

    ~RBTree() {
        destroy(root);
        delete Nil;
        Nil = nullptr;
    }

    RBTNode<T>* GetRoot() { return root; }

    bool Insert(const T& value) {
        RBTNode<T>* y = Nil;
        RBTNode<T>* x = root;

        // BST方式插入
        while (x != Nil) {
            if (value == x->key) return false;

            y = x;
            if (value < x->key) x = x->left;
            else x = x->right;
        }

        RBTNode<T>* z = NewNode(value);
        z->p = y;
        if (y == Nil) root = z;
        else if (z->key < y->key) y->left = z;
        else y->right = z;

        // 调整平衡
        InsertFixup(z);
        return true;
    }

    bool Remove(const T& key) {
        RBTNode<T>* t;
        if ((t = Search(root, key)) != Nil) return Remove(t);
        else return false;
    }

    RBTNode<T>* Search(RBTNode<T>* root, const T& key) const {
        if (root == Nil || root->key == key) return root;

        if (key < root->key) return Search(root->left, key);
        else return Search(root->right, key);
    }

protected:
    RBTNode<T>* NewNode(const T& x = T()) {
        RBTNode<T>* s = new RBTNode<T>();
        s->color = RBColor::RED;
        s->left = s->right = s->p = Nil;
        s->key = x;
        return s;
    }

    void LeftRotate(RBTNode<T>* x) {
        RBTNode<T>* y = x->right;
        x->right = y->left;

        if (y->left != Nil) y->left->p = x;

        y->p = x->p;

        if (root == x) root = y;
        else if (x == x->p->left) x->p->left = y;
        else x->p->right = y;

        y->left = x;
        x->p = y;
    }

    void RightRotate(RBTNode<T>* x) {
        RBTNode<T>* y = x->left;
        x->left = y->right;

        if (y->right != Nil) y->right->p = x;

        y->p = x->p;

        if (root == x) root = y;
        else if (x == x->p->left) x->p->left = y;
        else x->p->right = y;

        y->right = x;
        x->p = y;
    }

    void InsertFixup(RBTNode<T>* z) {
        RBTNode<T>* uncle;
        while (z->p->color == RBColor::RED) {
            if (z->p == z->p->p->left) {
                uncle = z->p->p->right;

                if (uncle->color == RBColor::RED) {
                    z->p->color = RBColor::BLACK;       // case 1
                    uncle->color = RBColor::BLACK;      // case 1
                    z->p->p->color = RBColor::RED;      // case 1
                    z = z->p->p;                        // case 1
                }
                else {
                    if (z == z->p->right) {
                        z = z->p;                       // case 2
                        LeftRotate(z);                  // case 2
                    }
                    z->p->color = RBColor::BLACK;       // case 3
                    z->p->p->color = RBColor::RED;      // case 3
                    RightRotate(z->p->p);               // case 3
                }
            }
            else if (z->p == z->p->p->right) {
                uncle = z->p->p->left;
                if (uncle->color == RBColor::RED) {
                    z->p->color = RBColor::BLACK;
                    uncle->color = RBColor::BLACK;
                    z->p->p->color = RBColor::RED;
                    z = z->p->p;
                }
                else {
                    if (z == z->p->left) {
                        z = z->p;
                        RightRotate(z);
                    }
                    z->p->color = RBColor::BLACK;
                    z->p->p->color = RBColor::RED;
                    LeftRotate(z->p->p);
                }
            }
        }
        root->color = RBColor::BLACK;
    }

    void Transplant(RBTNode<T>* u, RBTNode<T>* v) {
        if (u->p == Nil) root = v;
        else if (u == u->p->left) u->p->left = v;
        else u->p->right = v;

        v->p = u->p;
    }

    RBTNode<T>* Minimum(RBTNode<T>* x) {
        if (x->left == Nil) return x;
        return Minimum(x->left);
    }

    void RemoveFixup(RBTNode<T>* x) {
        while (x != root && x->color == RBColor::BLACK) {
            if (x == x->p->left) {
                RBTNode<T>* w = x->p->right;

                if (w->color == RBColor::RED) {
                    w->color = RBColor::BLACK;              // case 1
                    x->p->color = RBColor::RED;             // case 1
                    LeftRotate(x->p);                       // case 1
                    w = x->p->right;                        // case 1
                }
                if (w->left->color == RBColor::BLACK && w->right->color == RBColor::BLACK) {
                    w->color = RBColor::RED;                // case 2
                    x = x->p;                               // case 2
                }
                else {
                    if (w->right->color = RBColor::BLACK) {
                        w->color = RBColor::RED;            // case 3
                        w->left->color = RBColor::BLACK;    // case 3
                        RightRotate(w);                     // case 3
                        w = x->p->right;                    // case 3
                    }

                    w->color = w->p->color;                 // case 4
                    w->p->color = RBColor::BLACK;           // case 4
                    w->right->color = RBColor::BLACK;       // case 4
                    LeftRotate(x->p);                       // case 4
                    x = root;                               // case 4
                }
            }
            else {
                RBTNode<T> w = x->p->left;
                if (w->color == RBColor::RED) {
                    w->p->color = RBColor::RED;
                    w->color = RBColor::BLACK;
                    RightRotate(x->p);
                    w = x->p->left;
                }
                if (w->right->color == RBColor::BLACK && w->right->color == RBColor::BLACK) {
                    w->color = RBColor::RED;
                    x = x->p;
                }
                else {
                    if (w->left->color == RBColor::BLACK) {
                        w->right->color = RBColor::BLACK;
                        w->color = RBColor::RED;
                        LeftRotate(w);
                        w = x->p->left;
                    }

                    w->color = x->p->color;
                    x->p->color = RBColor::BLACK;
                    w->left->color = RBColor::BLACK;
                    RightRotate(x->p);
                    x = root;
                }
            }
        }
        x->color = RBColor::BLACK;
    }

    void Remove(RBTNode<T>* z) {
        RBTNode<T>* x = Nil;
        RBTNode<T>* y = z;
        RBColor ycolor = y->color;

        if (z->left == Nil) {
            x = z->right;
            Transplant(z, z->right);
        }
        else if (z->right == Nil) {
            x = z->left;
            Transplant(z, z->left);
        }
        else {
            y = Minimum(z->right);
            ycolor = y->color;
            x = y->right;

            if (y->p == z) x->p = y;
            else {
                Transplant(y, y->right);
                y->right = z->right;
                y->right->p = y;
            }
            Transplant(z, y);
            y->left = z->left;
            z->left->p = y;
            y->color = z->color;
        }

        if (ycolor == RBColor::BLACK) RemoveFixup(x);
    }

    void destroy(RBTNode<T>*& root) {
        if (root == Nil) return;
        destroy(root->left);
        destroy(root->right);
        delete root;
        root = nullptr;
    }

private:
    RBTNode<T>* root;
    RBTNode<T>* Nil; // 外部结点
};

main.cpp

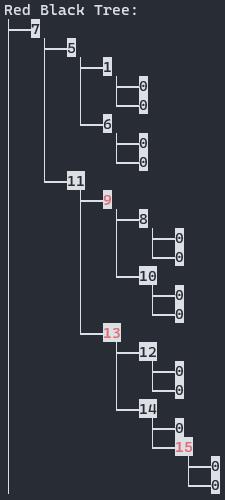
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>

#include "RBTree.h"

using namespace std;

template <typename T>
void PrintRBTreeAsDirectoryHelper(const RBTNode<T>* node, const string& prefix, bool is_left) {
    if (node == nullptr) {
        return;
    }

    string color_code;
    if (node->color == RBColor::RED) {
        color_code = "\033[0;47;31m";
    }
    else {
        color_code = "\033[0;47;30m";
    }

    cout << prefix;
    cout << (is_left ? "├──" : "└──");
    cout << color_code << node->key << "\033[0m" << endl;

    string new_prefix = prefix + (is_left ? "│   " : "    ");

    PrintRBTreeAsDirectoryHelper(node->left, new_prefix, true);
    PrintRBTreeAsDirectoryHelper(node->right, new_prefix, false);
}

template <typename T>
void PrintRBTreeAsDirectory(RBTree<T>& tree) {
    cout << "Red Black Tree: " << endl;
    PrintRBTreeAsDirectoryHelper(tree.GetRoot(), "", true);
}

int main() {
    RBTree<int> tree;
    int arr[] = { 1, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 };
    int n = sizeof(arr) / sizeof(int);
    for (auto n : arr) tree.Insert(n);

    PrintRBTreeAsDirectory(tree);

    return 0;
}

运行结果

二叉查找树和红黑树的区别以及时间、空间性能

TODO