实验要求
实现对数组[-2, 1, -3, 4, -1, 2, 1, -5, 4]的快速排序并画出流程图。
实现对数组[95, 94, 91, 98, 99, 90, 99, 93, 91, 92]的计数排序并画出流程图。
以上两种排序算法的区别有哪些?分别的时间和空间复杂度是多少?
实验原理
快速排序
快速排序的思想是任找一个元素作为基准,对待排数组进行分组,使基准元素左边的数据比基准数据要小,右边的数据比基准数据要大,这样基准元素就放在了正确的位置上。然后对基准元素左边和右边的组进行相同的操作,最后将数据排序完成。
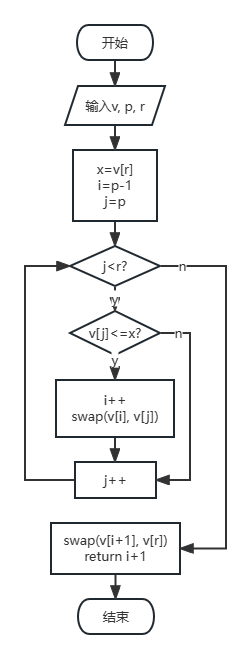
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 int partition (vector<int >& v, int p, int r) int x = v[r]; int i = p - 1 ; for (int j = p; j < r; j++) { if (v[j] <= x) { i++; swap (v[i], v[j]); } } swap (v[i + 1 ], v[r]); return i + 1 ; } void quick_sort (vector<int >& v, int p, int r) if (p < r) { int q = partition (v, p, r); quick_sort (v, p, q - 1 ); quick_sort (v, q + 1 , r); } }
partition:
计数排序
计数排序是由额外空间的辅助和元素本身的值决定的。计数排序过程中不存在元素之间的比较和交换操作,根据元素本身的值,将每个元素出现的次数记录到辅助空间后,通过对辅助空间内数据的计算,即可确定每一个元素最终的位置。
算法过程:
根据待排序集合中最大元素和最小元素的差值范围,申请额外空间;
遍历待排序集合,将每一个元素出现的次数记录到元素值对应的额外空间内;
对额外空间内数据进行计算,得出每一个元素的正确位置;
将待排序集合每一个元素移动到计算出的正确位置上。
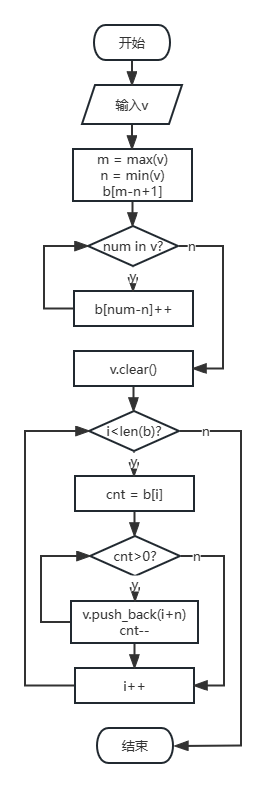
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 void counting_sort (vector<int >& v) int maxnum = *max_element (v.begin (), v.end ()); int minnum = *min_element (v.begin (), v.end ()); vector<int > b (maxnum - minnum + 1 ) ; for (auto n : v) { b[n - minnum]++; } v.clear (); for (int i = 0 ; i < b.size (); i++) { int cnt = b[i]; while (cnt--) { v.push_back (i + minnum); } } }
实验与结果
编写测试代码
加入辅助函数print_vector,创建好测试用例以及对照实验
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 #include <iostream> #include <vector> #include <string> #include <algorithm> using namespace std;void print_vector (string m, vector<int >& v) cout << m; for (auto n : v) { cout << n << " " ; } cout << endl; } int main () vector<int > v1{ -2 , 1 , -3 , 4 , -1 , 2 , 1 , -5 , 4 }; vector<int > v2{ 95 , 94 , 91 , 98 , 99 , 90 , 99 , 93 , 91 , 92 }; vector<int > v1_compare (v1) ; vector<int > v2_compare (v2) ; print_vector ("before quick sort: \t" , v1); quick_sort (v1, 0 , v1.size ()-1 ); print_vector ("after quick sort: \t" , v1); sort (v1_compare.begin (), v1_compare.end ()); print_vector ("after sort: \t\t" , v1_compare); print_vector ("before counting sort: \t" , v2); counting_sort (v2); print_vector ("after counting sort: \t" , v2); sort (v2_compare.begin (), v2_compare.end ()); print_vector ("after sort: \t\t" , v2_compare); return 0 ; }
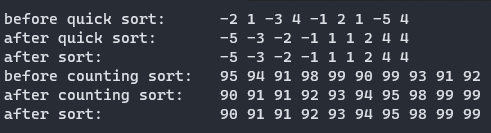
运行结果
实验分析
两种排序算法比较
快速排序基于分治的思想,每次处理会将一个元素放置到其最终的位置,是基于比较的算法,只要元素能够进行比较则可进行排序。
对于快速排序:2 )
对于计数排序: