Julia编程语言
TODO 由于Julia非常新,并且一直在更新,所以20年写的代码现在复现时会有环境问题,等有空了再继续写
20年的时候,由于工作需要,有编写一些脚本。包括自动编译脚本、日志分析脚本、证书生成脚本等。其中有些使用SHELL脚本实现,有些用Python编写。
但我都感觉没有完成地很漂亮:
- 一方面SHELL因为其通用性,对代码文件的处理比较暴力,如果后续修改代码的同事不知道哪些代码被自动编译脚本使用了,擅自修改的话,编译不通过都是小事,文件有可能被自动编译脚本改得乱七八糟。
- 另一方面Python这边有着Python2和Python3的混乱,导致维护旧的脚本得遵照Python2的规范;而且由于做嵌入式需要在不同平台来回转,Python的缩进式代码被几个编辑器保存过很有可能就乱掉了,非常不优雅。
可以吐槽的点还有很多,不过这篇文章主要是介绍我如何发现Julia语言并且用这个语言做了一些什么好玩的事情。
初识Julia
去了解了一下有哪些之前没有接触过的比较新的编程语言,相中了Rust和Julia。
先去学习的是Rust语言,这个语言很好,主打内存安全,如果学习熟练了用来做一些系统程序会降低很多后续的维护成本。编了几个程序下来,最大的感受就是编程的自由度降低了,写代码之前一直都得想着这样写是不是不能通过编译(应该是不够熟练Rust编程思想的问题)。
然后去学习了一下Julia,发现到处都是在夸它的,又说有像Python这样脚本语言的实时交互,又说性能与静态编译的C语言相媲美,还说对于多线程、分布式、多种编码格式都有非常好的支持。而且可以和其他语言混合使用,别的语言的成熟的库可以直接使用。瞬间被吸引了。
不过后面也觉得Julia还是有一些没有解决的问题的,最主要的就是它为了实现运行时性能,使用了LLVM,一般情况下还好说,但如果突然导入了一个非常大的库,那么等待LLVM编译的过程会让使用体验非常分割。
被Julia吸引
找了一些教程把Julia的基本语法学完了,期间也看到一些有意思的代码,比如说有一份文档叫做julia_express.pdf,在它的最后有一段这样的代码:
1 | 0:2e-3:2π .|>d->(P= |
它运行起来的效果是这样的(动图):

非常丝滑,非常好玩,我们可以从中看出Julia的以下特性:
- 排版非常自由、灵活
- 对Unicode编码天然的支持
- 对数学公式非常友好(比如可以直接使用
√来开根号,可以直接使用π等等) - 自动推导变量类型,避免了代码中很多不必要的字符
- 函数定义非常随性,让程序员专注于功能而非编码本身
- 矢量化计算减少了循环语句的编写,便于语言内部优化同时代码也很简洁
实践Julia
摩拳擦掌,急切想找一些途径来实践一下,先是把工作中使用到的脚本都用Julia再实现了一遍,发现Julia对于安全的随机数的支持非常好,而且因为可以和C语言混用,已经有人发布了Mbed-TLS的接口,密码算法也得到了很好的支持。
不得不说Julia的社区非常非常友好!因为Julia非常新,使用领域也集中于Data Science这种细分领域,所以现成的资料非常少,好在社区中有很多人会很乐意提供帮助。
不如用Julia来刷算法题吧!可惜之前常接触的平台,比如力扣,没有对Julia的支持。好在发现了另外一个平台,Codewars。不但语言支持得非常多,而且还支持用户将其他语言的算法题翻译成另外一种语言的题,实现其判题程序。
开刷!下班了就先刷几个题再回去。
几周之后,前三档难度的题被我刷空了!无奈只能开始刷简单的题,可是不够有成就感。
于是找到了一个很好玩的玩法:尽可能兼顾效率的同时,只用一行代码通过题目。
举几个例子:
举例1
看这一题:
1 | Take 2 strings s1 and s2 including only letters from a to z. |
很简单对吧?用很多方法都可以做出来,这里我们重点看一下我的解法:
1 | longest = join ∘ sort ∘ unique ∘ * |
是不是一脸问号?但如果知道了Julia语法之后,会发现这样写完全没有歧义,非常清晰!
上面的代码等价于这样(∘的作用其实就是连接函数,而Julia就是函数式编程):
1 | function longest(a, b) |
这种写法明显就多了很多括号,如果表达式非常复杂的时候,括号显然降低了很多代码的可读性,并且对于函数定义的function end,格式非常固定,需要多写很多字符,在这种一个表达式就可以写完的场景中,显然是非常多余的,所幸Julia提供了使用赋值号来定义函数的方式。
举例2
再看这一题,也是可以用内置方法的组合来完成任务的:
1 | Program a function sumAverage(arr) where arr is an array containing arrays full of numbers, for example: |
显然是一题模拟题,照着题目给的步骤做就行了,而这种正好就是日常编写脚本过程中最常用的场景。我的题解:
1 | sumaverage(arr) = arr .|> mean |> floor ∘ sum |
神奇地发现,对于一个二维数组的处理,居然不需要循环?!
其实秘诀就在于代码.|>中的点,这个点会告诉Julia,对于arr需要做矢量化运算,也就是将其所有成员分别做同样的操作。
那么代码流程就是:
- 将arr的所有元素(一维数组)传到mean函数中,mean函数能够接受一维数组并且求其均值
- 处理完之后的返回值是一个一维数组,这个一维数组里面是很多个平均值
- 将这个一维数组使用
|>运算符传到floor ∘ sum里面去
阅读起来,从左到右,非常顺畅,完全不需要去数括号。
举例3
如果内置函数不能直接完成任务呢?再来看这个例子:
1 | Common denominators |
我的题解为:
1 | convert_fracts(lst) = [big(i[1])//big(i[2]) for i in lst] |> r -> lcm(getfield.(r, :den)...) |> x -> [[x÷ra.den*ra.num, x] for ra in r] |
虽然有些强行一行的意味,因为定义了两个匿名函数。但是代码结构还是非常清晰的:
- 使用生成式创建分数数组
- 计算最小公倍数
- 使用生成式生成答案
图形相关
得益于Julia对数学公式的友好支持,绘制图表的工作在Julia中显得尤其得心应手。
绘制图表
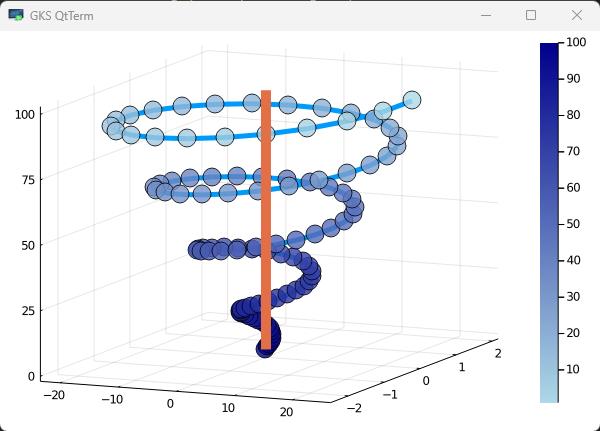
使用Plots库绘制三维平面上的曲线:
1 | using Plots |
使用Makie绘制曲面: