GAMES101笔记 - Resterization（光栅化）

系列文章
-> GAMES101笔记 - Resterization（光栅化）
GAMES101笔记 - Shading（着色）
GAMES101笔记 - Geometry（几何）

20年的时候，好朋友推荐了这个课程给我，简直是神仙课程！当时每天下班后就再花一个多小时来听一节课，陆陆续续听完了。最近打算重温一下这系列课程，顺便补上笔记。

图形学有一种魔力，每次学图形学相关的知识的时候，总在感叹其美妙。第一次系统地学习图形学是在大三，当时智能车已经进入了平稳的调试期，所以找了一些囤积起来的一直想学的技术书籍开始学习：Golang、图形学、Unity3D等等。
学到图形学的时候，正好智能车这边在调试利用陀螺仪对坡道的识别，所以突发奇想：在屏幕上显示一个3D图形，然后把陀螺仪解算出来的姿态实时绑定到3D图形上面，会比单纯地看上位机展示出来的陀螺仪数据曲线要来的直观很多吧！于是有了这个玩意：

---

线代知识点回顾

向量

$\begin{aligned} \vec{a} &= (x_a, y_a, z_a)^T \\ \vec{b} &= (x_b, y_b, z_b)^T \end{aligned}$

• 点乘：$\vec{a}·\vec{b} = |\vec{a}||\vec{b}|cosθ = x_a x_b + y_a y_b + z_a z_b$
• 叉乘：$\vec{a}×\vec{b} = (y_a z_b - y_b z_a, z_a x_b - x_a z_b, x_a y_b - y_a x_b)^T$
  $|\vec{a}×\vec{b}| = |\vec{a}||\vec{b}|sinθ$，方向垂直于$\vec{a}$和$\vec{b}$所在的平面，符合右手螺旋定则

点乘作用：

• 得到两个向量之间的夹角，特别是两个单位向量
• 找到一个向量对另一个向量的投影
• 符号表示“前”与“后”的信息
• 大小表示两个向量有多“接近”

叉乘作用：

• 判断点是否在三角形内（点P同时在三条边左边或右边）
• 获得坐标系

矩阵

• $M×N$的矩阵只能和$N×P$的矩阵相乘
• 矩阵相乘$AB=C$，其中$C$的$i$行$j$列元素是$A$的第$i$个行向量和$B$的第$j$个列向量点乘的值
• $AB = BA$通常不成立
• $(AB)^T = B^T A^T$（穿脱原则）
• $AA^{-1} = I$（矩阵的逆）
• $\vec{a}·\vec{b} = \vec{a}^T\vec{b}$
• $\vec{a}×\vec{b} = A^*\vec{b}$

变换

缩放：

$\begin{pmatrix} x' \cr y' \end{pmatrix} = \begin{pmatrix} s_x & 0 \cr 0 & s_y \end{pmatrix} \begin{pmatrix} x \cr y \end{pmatrix}$

$x$轴以$s_x$比例缩放，$y$轴以$s_y$比例缩放。$s_x$和$s_y$可以取负数，图像会翻转。

切变：

$\begin{pmatrix} x' \cr y' \end{pmatrix} = \begin{pmatrix} 1 & a \cr 0 & 1 \end{pmatrix} \begin{pmatrix} x \cr y \end{pmatrix}$

旋转（默认逆时针旋转）：

$\begin{pmatrix} x' \cr y' \end{pmatrix} = \begin{pmatrix} cosθ & -sinθ \cr sinθ & cosθ \end{pmatrix} \begin{pmatrix} x \cr y \end{pmatrix}$

线性变换

$\begin{aligned} x' = ax + by \\ y' = cx + dy \end{aligned}$

$\begin{pmatrix} x' \cr y' \end{pmatrix} = \begin{pmatrix} a & b \cr c & d \end{pmatrix} \begin{pmatrix} x \cr y \end{pmatrix}$

$x' = Mx$

齐次坐标

平移变换：

$\begin{pmatrix} x' \cr y' \end{pmatrix} = \begin{pmatrix} a & b \cr c & d \end{pmatrix} \begin{pmatrix} x \cr y \end{pmatrix} + \begin{pmatrix} t_x \cr t_y \end{pmatrix}$

与上面的$x' = Mx$形式不一样了，导致平移变换变得需要特殊处理，所以引入齐次坐标。

齐次坐标下：
二维的点：$(x, y, 1)^T$
二维向量：$(x, y, 0)^T$

平移变换变成了：

$\begin{pmatrix} x' \cr y' \cr w' \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \cr 0 & 1 & t_y \cr 0 & 0 & 1 \end{pmatrix} · \begin{pmatrix} x \cr y \cr 1 \end{pmatrix} = \begin{pmatrix} x + t_x \cr y + t_y \cr 1 \end{pmatrix}$

回到了$x' = Mx$的形式。

向量的齐次坐标为$0$，是因为向量具有平移不变性：

$\begin{pmatrix} x' \cr y' \cr w' \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \cr 0 & 1 & t_y \cr 0 & 0 & 1 \end{pmatrix} · \begin{pmatrix} x \cr y \cr 0 \end{pmatrix} = \begin{pmatrix} x \cr y \cr 0 \end{pmatrix}$

齐次坐标下，以下有意义的运算天然成立：
向量 + 向量 = 向量
点 - 点 = 向量
点 + 向量 = 点

而对于点+点，我们定义：

$\begin{pmatrix} x \cr y \cr w \end{pmatrix} \iff \begin{pmatrix} x/w \cr y/w \cr 1 \end{pmatrix} , (w ≠ 0)$

这个定义下，点+点变成了两个点的中点。

有了齐次坐标，我们所有的变换都可以写为如下的仿射变换了：

$\begin{pmatrix} x' \cr y' \cr 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x \cr c & d & t_y \cr 0 & 0 & 1 \end{pmatrix} · \begin{pmatrix} x \cr y \cr 1 \end{pmatrix}$

变换组合

• 逆变换：$x = M^{-1}Mx$
• 不以原点为中心旋转：组合平移和旋转
• 变换的顺序很重要
• 先线性变换，再平移

三维变换

$\begin{pmatrix} x' \cr y' \cr z' \cr 1 \end{pmatrix} = \begin{pmatrix} a & b & c & t_x \cr d & e & f & t_y \cr g & h & i & t_z \cr 0 & 0 & 0 & 1 \end{pmatrix} · \begin{pmatrix} x \cr y \cr z \cr 1 \end{pmatrix}$

旋转：

$R_x(α) = \begin{pmatrix} 1 & 0 & 0 & 0 \cr 0 & cosα & -sinα & 0 \cr 0 & sinα & cosα & 0 \cr 0 & 0 & 0 & 1 \end{pmatrix}$

$R_y(α) = \begin{pmatrix} cosα & 0 & sinα & 0 \cr 0 & 1 & 0 & 0 \cr -sinα & 0 & cosα & 0 \cr 0 & 0 & 0 & 1 \end{pmatrix}$

$R_z(α) = \begin{pmatrix} cosα & -sinα & 0 & 0 \cr sinα & cosα & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \end{pmatrix}$

Rodrigues’ Rotation Formula:
（$\mathbf{n}$为旋转轴）

$R(\mathbf{n}, α) = cos(α)\mathbf{I} + (1-cos(α))\mathbf{nn^T} + sin(α) \underset{\mathbf{N}}{ \underbrace{ \begin{pmatrix} 0 & -n_z & n_y \cr n_z & 0 & -n_x \cr -n_y & n_x & 0 \end{pmatrix} } }$

四元数

为了解决旋转与旋转之间的插值而引入的。

---

观测变换（Viewing Transformation）

• model transformation
• view transformation
• projection transformation

视图变换（View / Camera Transformation）

定义相机：

• Position: $\vec{e}$
• Look-at / gaze direction: $\hat{g}$
• Up direction: $\hat{t}$

实际上是将相机放在原点，朝$-z$方向看（右手系），向上方向是$y$，将其他所有物体移动到相机的相对位置然后渲染。将移动和旋转分为两个矩阵来写，注意先移动后旋转：$M_{view} = R_{view} T_{view}$

• 移动到原点：

$T_{view} = \begin{pmatrix} 1 & 0 & 0 & -x_e \cr 0 & 1 & 0 & -y_e \cr 0 & 0 & 1 & -z_e \cr 0 & 0 & 0 & 1 \end{pmatrix}$

• 将$\hat{g}$旋转到$-Z$，$\hat{t}$旋转到$Y$，$(\hat{g}×\hat{t})$旋转到$X$。可是直接写该旋转矩阵有些困难，所以先写出其逆矩阵，也就是将$X$旋转到$(\hat{g}×\hat{t})$，其他轴同理。

$R^{-1}_{view} = \begin{pmatrix} x_{\hat{g}×\hat{t}} & x_t & x_{-g} & 0 \cr y_{\hat{g}×\hat{t}} & y_t & y_{-g} & 0 \cr z_{\hat{g}×\hat{t}} & z_t & z_{-g} & 0 \cr 0 & 0 & 0 & 1 \end{pmatrix} ⇒ R_{view} = \begin{pmatrix} x_{\hat{g}×\hat{t}} & y_{\hat{g}×\hat{t}} & z_{\hat{g}×\hat{t}} & 0 \cr x_t & y_t & y_t& 0 \cr x_{-g} & y_{-g} & z_{-g} & 0 \cr 0 & 0 & 0 & 1 \end{pmatrix}$

（正交矩阵符合公式$A^{-1}=A^T$）

投影变换（Projection transformation）

正交投影（定义一个立方体$[l, r]×[b, t]×[f, n]$，将其中心平移到原点，再三轴缩放到$[-1, 1]$）：

$M_{ortho} = \begin{pmatrix} {2 \over r-l} & 0 & 0 & 0 \cr 0 & {2 \over t-b} & 0 & 0 \cr 0 & 0 & {2 \over n-f} & 0 \cr 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -{r+l \over 2} \cr 0 & 1 & 0 & -{t+b \over 2} \cr 0 & 0 & 1 & -{n+f \over 2} \cr 0 & 0 & 0 & 1 \end{pmatrix}$

透视投影（近平面比远平面小，所以把远平面挤压到跟近平面一样大就可以使用正交投影了）：
（使用相似三角形推导，推导略）

$M_{persp} = M_{ortho}M_{persp→ortho} = M_{ortho} \begin{pmatrix} n & 0 & 0 & 0 \cr 0 & n & 0 & 0 \cr 0 & 0 & n+f & -nf \cr 0 & 0 & 1 & 0 \end{pmatrix}$

使用field-of-view(fovY)和宽高比(aspect ratio)来定义一个视锥。

Viewport transform matrix

用来将$[-1, 1]$范围内的内容拉伸到宽为width，高为height的显示区域内。

$M_{viewport} = \begin{pmatrix} {width \over 2} & 0 & 0 & {width \over 2} \cr 0 & {height \over 2} & 0 & {height \over 2} \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \end{pmatrix}$

光栅化

• 像素是一个个小方块，左下角坐标为$(0, 0)$，像素点中心坐标为$(x+0.5, y+0.5)$
• 通过采样获得像素点颜色
• 使用叉乘来判断是否像素点中心在三角形内部
• 只有在三角形包围盒内的像素才需要判断是否在三角形内

抗锯齿（反走样）

锯齿是 Sampling Artifacts 中的一种，Sampling Artifacts 包括：

• Jaggies（锯齿）
• Moire（摩尔纹）
• 反转的轮子（时间采样）
• …

走样产生

• 同样的采样频率，有可能在不同频率的信号上采样出来的结果完全相同，导致我们无法区分出这个采样结果来自于哪一个信号，所以产生了走样
• 对图像做傅里叶变换，会看到有“十字”形状的两条亮线，这是因为做傅里叶变换时会将图像拼接很多张，而接合的部分会产生一个高频信号
• 时域做卷积$\iff$频域做乘积
• 采样就是在重复某个频率的内容（使用周期的$\delta$函数与原信号相乘），如果采样频率较小，重复的频谱之间相距越近，如果重复的频谱之间有重叠，就出现了走样

反走样（Antialiasing / AA）

（核心就是降低信号频率或者提升采样频率）

• 增加采样率（比如硬件上增加分辨率）
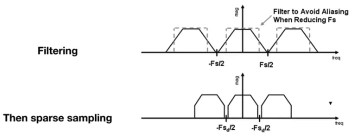
• 采样之前先做模糊（或者说滤波），低通滤波会将原始信号的频谱变窄，这样采样重复频谱的过程中就会让重叠部分减少，甚至不重叠
  

使用1像素大小的卷积核对原始图像的颜色做卷积（但实际得用一些近似方法）：

• MSAA (Multisample AA)，假设每一个像素里面有4×4的16个小像素，使用这16个位置对图像做模糊，缺点是因为需要多用很多点来探测是否在三角形内，计算量大
  工业上增加的点的排布会有各种不同方式
• FXAA (Fast Approximate AA)，先得到有锯齿的图，再找到图像的边界，替换这些边界为无锯齿的版本
• TAA (Temporal AA)，不同时间使用像素的不同位置采样，把MSAA的操作分散在了时间上

深度缓存（Z-buffer）

画家算法：先画远处的物体，后画近处的物体，近处的物体会将远处的物体遮挡。需要三角形按照深度排序，但是如果三角形交叉时候无法排序。

所以引入深度缓存，对每一个像素记录其深度，而不是三角形。绘制时，遍历所有三角形，当找到某个像素点在三角形内时，先判断这个像素点在三角形上的深度，是否与Z-buffer中已有的深度相比较小，如果是则说明这个像素会遮挡已经绘制好的像素点，所以需要更新frame-buffer中对应像素点的值，以及该像素点在Z-buffer中的值。

---

作业0

1. 配置环境
2. 给定一个点 P=(2,1), 将该点绕原点先逆时针旋转 45◦，再平移 (1,2), 计算出变换后点的坐标（要求用齐次坐标进行计算）。

配置环境

使用Ubuntu-22.04来编译运行代码框架，安装C++编译环境：
sudo apt-get install build-essential gdb make git

安装cmake:
sudo apt-get install cmake

安装eigen库：
sudo apt install libeigen3-dev

题解

添加代码：
main.cpp - function main

std::cout << "\nAssignment 0: " << std::endl;
Eigen::Vector3f p(2.0f, 1.0f, 1.0f);
Eigen::Matrix3f rotate, move;
float cos45 = std::cos(45.0/180.0*acos(-1));
float sin45 = std::sin(45.0/180.0*acos(-1));
rotate <<   cos45,  -sin45, 0.0, 
            sin45,  cos45,  0.0,
            0.0,    0.0,    1.0;
move << 1.0, 0.0, 1.0, 
        0.0, 1.0, 2.0, 
        0.0, 0.0, 1.0;
std::cout << move * rotate * p << std::endl;

结果

获得输出：

Assignment 0:
1.70711
4.12132
      1

---

作业1

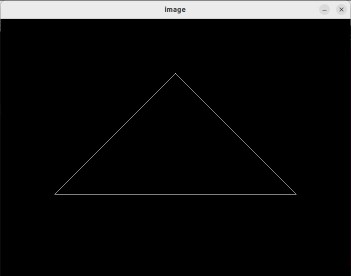
本次作业的任务是填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个点 v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0), 你需要将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形 (在代码框架中，我们已经提供了 draw_triangle 函数，所以你只需要去构建变换矩阵即可)。

环境配置

安装opencv：
sudo apt-get install libopencv-dev python3-opencv

题解

get_model_matrix只有一个float类型的旋转角度参数，所以只需返回一个关于$z$轴旋转的旋转矩阵即可：
main.cpp

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.
    float cos_angle = std::cos(rotation_angle * MY_PI / 180.0);
    float sin_angle = std::sin(rotation_angle * MY_PI / 180.0);
    Eigen::Matrix4f rotation;
    rotation << cos_angle,  -sin_angle, 0,  0,
                sin_angle,  cos_angle,  0,  0,
                0,          0,          1,  0,
                0,          0,          0,  1;

    return rotation * model;
}

get_projection_matrix给了视角、宽高比以及远近平面的$z$坐标，我们可以用虎书中给的矩阵：

$M_{proj} = \begin{pmatrix} -{1 \over [ktan({α \over 2})]} & 0 & 0 & 0 \cr 0 & -{1 \over tan({α \over 2})} & 0 & 0 \cr 0 & 0 & {n+f \over n-f} & {2nf \over n-f} \cr 0 & 0 & 1 & 0 \end{pmatrix}$

不过我这里想跟着老师的推导思路，将视锥先挤压成矩形，然后利用正交投影：
main.cpp

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    // Students will implement this function

    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the projection matrix for the given parameters.
    // Then return it.
    // [l, r]×[b, t]×[f, n]
    float angle = eye_fov * MY_PI / 180.0;
    float t = std::tan(angle / 2.0) * (-zNear);
    float b = -t;
    float r = t * aspect_ratio;
    float l = -r;

    Eigen::Matrix4f M_ortho_move, M_ortho_scale;
    M_ortho_move << 1,  0,  0,  -(r+l)/2.0,
                    0,  1,  0,  -(t+b)/2.0,
                    0,  0,  1,  -(zNear+zFar)/2.0,
                    0,  0,  0,  1;
    M_ortho_scale <<2.0/(r-l),  0,          0,                  0,
                    0,          2.0/(t-b),  0,                  0,
                    0,          0,          2.0/(zNear-zFar),   0,
                    0,          0,          0,                  1;
    Eigen::Matrix4f M_persp2ortho;
    M_persp2ortho <<zNear,  0,      0,          0,
                    0,      zNear,  0,          0,
                    0,      0,      zNear+zFar, -zNear*zFar,
                    0,      0,      1,          0;

    return M_ortho_move * M_ortho_scale * M_persp2ortho * projection;
}

结果

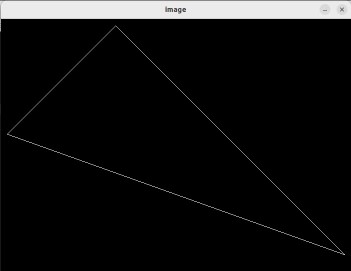
按下A或者D键会分别左右旋转一定角度。

提高部分

使用Rodrigues’ Rotation Formula：
main.cpp

Eigen::Matrix4f get_rotation(Vector3f axis, float angle)
{
    angle = angle * MY_PI / 180.0;
    Eigen::Matrix3f N;
    N <<0,          -axis.z(),  axis.y(),
        axis.z(),   0,          -axis.x(),
        -axis.y(),  axis.x(),   0;
    Eigen::Matrix3f R = std::cos(angle) * Eigen::Matrix3f::Identity() + 
                        (1-std::cos(angle))*axis*axis.transpose() + 
                        std::sin(angle) * N;
    
    Eigen::Matrix4f rotation = Eigen::Matrix4f::Zero();
    rotation(3, 3) = 1;
    rotation.block(0, 0, 2, 2) = R.block(0, 0, 2, 2);

    return rotation;
}

将main函数中的
r.set_model(get_model_matrix(angle));
修改为
r.set_model(get_rotation(Eigen::Vector3f(-1, 1, 0), angle));
让三角形绕着$(-1, 1, 0)$轴旋转：

---

作业2

在上次作业中，虽然我们在屏幕上画出一个线框三角形，但这看起来并不是那么的有趣。所以这一次我们继续推进一步——在屏幕上画出一个实心三角形，换言之，栅格化一个三角形。

题解

对于projection矩阵，我们这次直接用推导完成的矩阵：
main.cpp

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
{
    // TODO: Copy-paste your implementation from the previous assignment.
    Eigen::Matrix4f projection;
    eye_fov = eye_fov * MY_PI / 180.0;
    float ty = -1.0 / std::tan(eye_fov / 2.0);
    projection <<   (ty / aspect_ratio),    0,  0,  0,
                    0,                      ty, 0,  0,
                    0,                      0,  (zNear+zFar)/(zNear-zFar),  (-2.0*zNear*zFar)/(zNear-zFar),
                    0,                      0,  1,  0;

    return projection;
}

对于栅格化三角形，其步骤为：

1. 找到三角形的包围盒
2. 遍历包围盒中的像素，判断各像素是否在三角形内部
3. 如果是，则获得该像素在三角形中的深度值，并判断该深度值是否比现存Z-buffer中的小
4. 若新的z值较小，则更新frame-buffer和Z-buffer

rasterizer.cpp

//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
    auto v = t.toVector4();
    
    // TODO : Find out the bounding box of current triangle.
    // iterate through the pixel and find if the current pixel is inside the triangle
    float x_min = floor(std::min(std::min(v[0].x(), v[1].x()), v[2].x()));
    float x_max = ceil(std::max(std::max(v[0].x(), v[1].x()), v[2].x()));
    float y_min = floor(std::min(std::min(v[0].y(), v[1].y()), v[2].y()));
    float y_max = ceil(std::max(std::max(v[0].y(), v[1].y()), v[2].y()));

    // If so, use the following code to get the interpolated z value.
    //auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
    //float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
    //float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
    //z_interpolated *= w_reciprocal;

    // TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
    for (int x = x_min; x < x_max; x++) {
        for (int y = y_min; y < y_max; y++) {
            if (insideTriangle(x+0.5f, y+0.5f, t.v)) {
                auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
                float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                z_interpolated *= w_reciprocal;
                if (z_interpolated < depth_buf[get_index(x, y)]) {
                    Eigen::Vector3f point(x, y, 1.0f);
                    set_pixel(point, t.getColor());
                    depth_buf[get_index(x, y)] = z_interpolated;
                }
            }
        }
    }
}

判断一个点是否在三角形内，使用叉乘：即将各顶点与该点连成向量，将各向量与各边进行叉乘，结果的z值代表了叉乘之后的方向，如果三次叉乘都同向则说明点在三角形内。
rasterizer.cpp

static bool insideTriangle(int x, int y, const Vector3f* _v)
{   
    // TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
    Eigen::Vector3f ab(_v[0].x() - _v[1].x(), _v[0].y() - _v[1].y(), 1.0f);
    Eigen::Vector3f bc(_v[1].x() - _v[2].x(), _v[1].y() - _v[2].y(), 1.0f);
    Eigen::Vector3f ca(_v[2].x() - _v[0].x(), _v[2].y() - _v[0].y(), 1.0f);

    Eigen::Vector3f ap(_v[0].x() - x, _v[0].y() - y, 1.0f);
    Eigen::Vector3f bp(_v[1].x() - x, _v[1].y() - y, 1.0f);
    Eigen::Vector3f cp(_v[2].x() - x, _v[2].y() - y, 1.0f);

    float z1 = ab.cross(ap).z();
    float z2 = bc.cross(bp).z();
    float z3 = ca.cross(cp).z();

    return (z1 > 0 && z2 > 0 && z3 > 0) || (z1 < 0 && z2 < 0 && z3 < 0);
}

结果

提高部分

提高部分要求用SSAA，而课堂上讲的是MSAA。区别在于：

• MSAA (Multisample AA) 是利用每个像素点中多个点进行采样，达到“模糊”的目的，之后再将像素点中心的颜色显示出来。
• SSAA (Supersampling AA) 相当于渲染了一张更高分辨率的图片，然后将一个像素覆盖的几个子像素做平均，再显示。

增加SSAA所需要维护的子像素缓冲，顺便加一个开关方便后续对比：
rasterizer.hpp - class rasterizer

class rasterizer
{
public:
    rasterizer(int w, int h, bool use_2xSSAA = false);
private:
    bool enable_2xSSAA;
    std::vector<Eigen::Vector3f> frame_buf;
    std::vector<std::vector<Eigen::Vector3f>> frame_buf_2xSSAA;

    std::vector<float> depth_buf;
    std::vector<std::vector<float>> depth_buf_2xSSAA;
};

增加对每个子像素都进行处理的代码：
rasterizer.cpp - function rst::rasterizer::rasterize_triangle

std::vector<float> coord_offset{0.25, 0.75};
for (int x = x_min; x < x_max; x++) {
    for (int y = y_min; y < y_max; y++) {
        if (enable_2xSSAA) {
            int idx = 0;
            for (auto i : coord_offset) {
                for (auto j : coord_offset) {
                    if (insideTriangle(x+i, y+j, t.v)) {
                        auto[alpha, beta, gamma] = computeBarycentric2D(x+i, y+j, t.v);
                        float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                        float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                        z_interpolated *= w_reciprocal;
                        if (z_interpolated < depth_buf_2xSSAA[get_index(x, y)][idx]) {
                            frame_buf_2xSSAA[get_index(x, y)][idx] = t.getColor();
                            depth_buf_2xSSAA[get_index(x, y)][idx] = z_interpolated;
                        }
                    }
                    idx++;
                }
            }
        } else {
            if (insideTriangle(x+0.5f, y+0.5f, t.v)) {
                auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
                float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                z_interpolated *= w_reciprocal;
                if (z_interpolated < depth_buf[get_index(x, y)]) {
                    Eigen::Vector3f point(x, y, 1.0f);
                    set_pixel(point, t.getColor());
                    depth_buf[get_index(x, y)] = z_interpolated;
                }
            }
        }
    }
}

新增加的两个缓存也需要做初始化以及初值填充：
rasterizer.cpp

void rst::rasterizer::clear(rst::Buffers buff)
{
    if ((buff & rst::Buffers::Color) == rst::Buffers::Color)
    {
        std::fill(frame_buf.begin(), frame_buf.end(), Eigen::Vector3f{0, 0, 0});
        if (enable_2xSSAA) {
            for (int i = 0; i < frame_buf_2xSSAA.size(); i++) {
                frame_buf_2xSSAA[i].resize(4);
                std::fill(frame_buf_2xSSAA[i].begin(), frame_buf_2xSSAA[i].end(), Eigen::Vector3f{0, 0, 0});
            }
        }
    }
    if ((buff & rst::Buffers::Depth) == rst::Buffers::Depth)
    {
        std::fill(depth_buf.begin(), depth_buf.end(), std::numeric_limits<float>::infinity());
        if (enable_2xSSAA) {
            for (int i = 0; i < depth_buf_2xSSAA.size(); i++) {
                depth_buf_2xSSAA[i].resize(4);
                std::fill(depth_buf_2xSSAA[i].begin(), depth_buf_2xSSAA[i].end(), std::numeric_limits<float>::infinity());
            }
        }
    }
}

rst::rasterizer::rasterizer(int w, int h, bool use_2xSSAA) : width(w), height(h), enable_2xSSAA(use_2xSSAA)
{
    frame_buf.resize(w * h);
    depth_buf.resize(w * h);
    if (enable_2xSSAA) {
        frame_buf_2xSSAA.resize(w * h);
        depth_buf_2xSSAA.resize(w * h);
    }
}

实际显示时，需要对子像素做平均：
rasterizer.cpp - function rst::rasterizer::draw

rasterize_triangle(t);
if (enable_2xSSAA) {
    for (int x = 0; x < width; x++) {
        for (int y = 0; y < height; y++) {
            Eigen::Vector3f color(0, 0, 0);
            for (int i = 0; i < 4; i++) {
                color += frame_buf_2xSSAA[get_index(x, y)][i];
            }
            color /= 4;
            set_pixel(Eigen::Vector3f(x, y, 1.0f), color);
        }
    }
}

最后修改main函数中的逻辑：
main.cpp - function main

rst::rasterizer r(700, 700, false);

while(key != 27)
{
    long long frame_begin_time = get_timestamp();

    // ...

    long long frame_time = get_timestamp() - frame_begin_time;
    std::cout << "frame count: " << frame_count++ << " duration: " << frame_time << '\n';
}

添加时间戳函数：
main.cpp

#include <sys/time.h>
#include <time.h>

long long get_timestamp(void)
{
    long long tmp;
    struct timeval tv;

    gettimeofday(&tv, NULL);
    tmp = tv.tv_sec;
    tmp = tmp * 1000;
    tmp = tmp + (tv.tv_usec / 1000);

    return tmp;
}

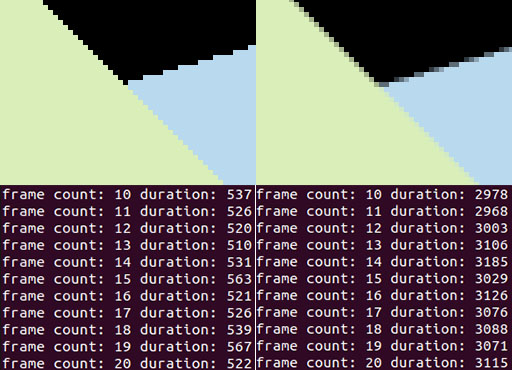
结果：

将抗锯齿开启与不开启的图像做对比，效果还是非常显著的（效率下降也是非常显著的）：