GAMES101笔记 - Geometry（几何）

系列文章
GAMES101笔记 - Resterization（光栅化）
GAMES101笔记 - Shading（着色）
-> GAMES101笔记 - Geometry（几何）

Ways to Represent Geometry

隐式（Implicit）几何

通过描述点之间的关系来确定几何。例如单位球的隐式表示： $x^2+y^2+z^2=1$ 。
定义函数 $f(x,y,z)=0$ ，在隐式几何表示中，只要找到点满足该函数，则说明该点在几何上。

缺点：难以描述复杂形状。
优点：

容易表述。
容易查询（内/外、点到表面的距离）。
容易做光线求交。
对简单形状友好，没有走样。
容易处理拓扑变化。

表示方式：

Algebraic Surfaces（代数表示）。
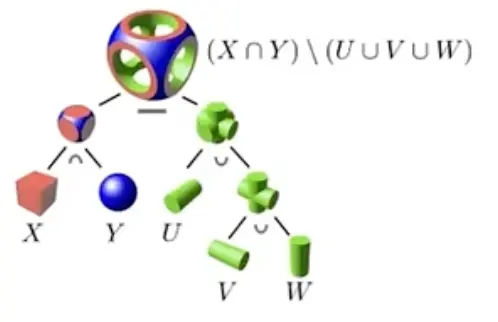
Constructive Solid Geometry (CSG)：将隐式表示的几何通过布尔运算组合起来。
Distance Functions（距离函数）：通过描述空间中任何点到平面的最近距离俩表示几何。
- 通过 blend 距离函数，可以得到像是水滴融合的效果。
- 表示能力非常强。
- 水平集方法（Level Set Methods）用图的像素来表示距离函数（像是等高线）。
Fractals（分形）。

显式（Explicit）几何

所有点直接给出（像是用三角形面表示），或者通过参数映射（parameter mapping）的方法给出。
参数映射的方法，就是通过坐标 $(u,v)$ 可以得到坐标 $(x,y,z)$ ，只要遍历一遍所有 $(u,v)$ ，就可以得到几何的所有点。

缺点：不方便判断点在表面内/外。
优点：容易得知几何的形状。

表示方式：

Point Cloud（点云）：一个 $(x,y,z)$ $(x, y, z)$ 的列表。
- 容易表示任何几何，但是需要非常的数据量。
- 常用来转换成多边形表面。
- 如果点云稀疏，则难以绘制。
Polygon Mesh（多边形面）：多用三角形或者四边形。
- 数据结构比较复杂。
- 几乎是最广泛运用的表示方式。
- 例如.obj文件格式（Wavefront Object File）。

Curves（曲线）

Bézier Curves（贝塞尔曲线）

属于显式表示。

使用 de Casteljau Algorithm 算法来绘制贝塞尔曲线。

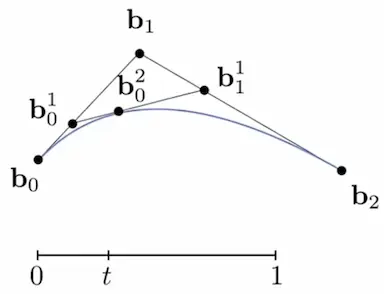
对于三个点的情况（ $b_0$ 、 $b_1$ 和 $b_2$ 所决定的曲线）。假设有一个参数 $t$ ，它从 0 逐渐变到 1 的过程中，我们将 $\overline{b_0 b_1}$ 和 $\overline{b_1 b_2}$ 比例为 t 处的点连起来，得到线段 $\overline{b_0^1 b_1^1}$ ，再取 $\overline{b_0^1 b_1^1}$ 比例为 t 处的点 $b_0^2$ ，该点则为最终所要绘制的曲线上的点。

对于四个点的情况，先取所有线段中比例为 t 处的点，依次连接起来，新的点只有三个，就转化成了上述三个点的情况。

这里可以看到创建贝塞尔曲线的动画演示。

代数表示

b^n(t) = b_0^n(t) = \sum_{j=0}^n{b_jB_j^n(t)}

其中 $B_i^n(t)$ 叫做伯恩斯坦多项式（Bernstein polynomials）。

B_i^n(t) = \begin{pmatrix} n \cr i \end{pmatrix} t^i(1-t)^{n-i}

使用这种插值方式，三维也可以同样生效。

性质

必须过起点和终点。
四个控制点时，起始位置切线是 $3(b_1-b_0)$ 的方向，结束位置同理。
对不同的顶点做仿射变换，再绘制出的曲线，和绘制出曲线之后，再做仿射变换，得到的结果是一样的。
但对投影就不一定成立了。
绘制出的曲线一定在控制点形成的凸包内。

Piecewise Bézier Curves（逐段的贝塞尔曲线）

控制点多的时候不好操作。

用的最多的是 Piecewise cubic Bézier，也就是四个控制点的情况。把各段曲线连接起来，就成了最终的结果。（就像钢笔工具）

如果要使得连接点连续，需要让前一段最后两个点组成的线段与后一段前两个点组成的线段方向相同，长度相等（即曲线导数光滑）。

$C^0$ 连续：只需几何上连在一起。
$C^1$ 连续：切线也连续。
…

其他样条（splines）

样条：一个可控的曲线。

B-splines（B-样条）：对贝塞尔曲线的扩展。
- 有布局性。
- 非常复杂。
- NURBS（非均匀有理 B-样条）

Surfaces（曲面）

Bézier Surfaces（贝塞尔曲面）

在两个方向上分别创造贝塞尔曲线。可以通过遍历 $(u,v)$ 的方式。

Geometry Processing（几何处理）

Mesh subdivision（网格细分）
Mesh simplification（网格简化）
Mesh regularization（网格正则化）

网格细分

引入更多三角形。
让三角形位置发生变化，让模型更光滑。

Loop Subdivision（Loop 细分）：

适用于三角形网格。

三角形每条边取中点，分别连接起来，一个三角形变成四个。
对于新/旧顶点分别用不同的规则去移动。
对于新顶点，用如下公式插值： ${3 \over 8}(A+B)+{1 \over 8}(C+D)$
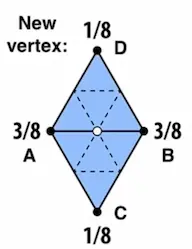
对于旧顶点，使用与它直接相连的旧顶点的位置平均，以及自身的旧位置。对这两个值做加权平均，得到新位置。

Catmull-Clark Subdivision：

适用于一般网格。

定义：

Quad face：四边形面。
Non-quad face：非四边形面。
Extraordinary vertex：奇异点，度不为 4 的点。

步骤：

取每条边的中点，和每个面中心的点，将面中心的点与边中心的点连起来。
原先有多少个非四边形面，就会引入多少个奇异点，面全部变成四边形面。
点区分成三类：面中心的点、边中心的点和旧的点。
面中心的点是面顶点的平均。
边中心的点是边的顶点以及这条边对应两个面的中心点的平均。
旧的点用和他相连的旧的点只和的两倍，以及与它相连的面的中心点，还有它本身的4倍做平均。

网格简化

Edge collapsing（边坍缩）：

找到一条边，将其连接的两个顶点放到一起。

使用 Quadric Error Metrics（二次度量误差）来定义一个优化问题。求一个点到原本的几个面的距离的平方和达到最小。

计算出所有边坍缩之后的二次度量误差，从误差小的边开始坍缩，直到满足简化要求。

但有问题，因为坍缩会影响别的边。用堆来减小这种影响带来的代价。

作业

TODO: homework